This tutorial demonstrates how to model a Susceptible-Infected (SI)
epidemic in an open population. An example of an SI epidemic is HIV,
with infected persons never leaving the infected stage before mortality.
Modeling HIV is quite complicated, and this tutorial is not meant to be
a full-scale HIV model per se: it does not include many
components of HIV models, such as disease stage, drug therapy, and so
on. This only represents SI dynamics generally with the possibility of
vital dynamics.
The population is open as we are now including arrivals and
departures in the epidemic process. Simulating an epidemic in an open
population requires adjustments that accommodate changes to the network
structure over time. For the sake of simplicity, the departure processes
will not depend on disease status, which will keep the population size
stable over time.
This tutorial will include two counterfactual network models that
will allow behavior (mean degree and mixing) to vary across two
hypothetical risk groups. These behavioral differences might represent
different demographic groups (e.g., younger persons and older
persons).
Network Model
The network is initialized as before, but now we set a vertex
attribute of risk group onto the network. Risk group will be a binary
variable, with the risk groups evenly sized in the population.
nw <- network_initialize(n = 500)
nw <- set_vertex_attribute(nw, attrname = "risk", value = rep(0:1, each = 250))
We will proceed by fitting two network models: Model 1 will feature a
scenario in which the mean degree is the same in both risk groups and
there is no risk group homophily; Model 2 will feature a scenario in
which Risk Group 1 has a higher mean degree and there is strong
assortative mixing.
Model 1: Random Mixing, Degree
The first model will assume that there is random mixing in the
population, with no preference for same-risk partnerships, and that the
two risk groups have the same mean degree. In fact, this means that
there is no need to include separate terms for degree and homophily in
the network model (it is an edges-only model or Bernoulli random
graph).
Parameterization
The formation formula for this first model will only include a term
for edges. We will use edges to parameterize the overall
mean degree in the network.
formation <- ~edges
The target statistics for each of the terms is as follows. Both Model
1 and Model 2 will use the same mean degree in the population overall: a
0.5 mean degree, which translates into 125 edges in a population of 500
nodes.
target.stats <- 125
The dissolution model components will be the same for both models. We
specify a homogeneous dissolution model with an average relational
duration of 40 weeks. The dissolution coefficients must be adjusted to
accommodate the exogenous probability of edge dissolution due to
mortality (or other forms of nodal departure). This adjustment has the
impact of increasing the coefficient as seen below. Recall that this is
because the dissolution model is actually implemented as a persistence
model, so a larger coefficient means longer partnerships.
coef.diss <- dissolution_coefs(dissolution = ~offset(edges),
duration = 40, d.rate = 0.001)
coef.diss
Dissolution Coefficients
=======================
Dissolution Model: ~offset(edges)
Target Statistics: 40
Crude Coefficient: 3.663562
Mortality/Exit Rate: 0.001
Adjusted Coefficient: 3.7469
The d.rate parameter here is the average mortality (or
other departure) rate per time step. This will correspond to the
epidemic parameters specified below in param.net. In the
case that there is disease-induced mortality, this parameter should
represent a weighted average of the different departure rates in the
full system. It is often challenging to calculate this in advance
because disease prevalence and thus disease-induced mortality changes
over time. Therefore, research-level models often use some trial and
error to specify this parameter.
In this tutorial example a d.rate parameter of 0.001
corresponds to an average “lifespan” (time spent in the population) of
1/0.001 = 1000 timesteps. This is probably unrealistic for
most disease models (especially since the average relations last 40 time
steps), but we are using a large value for demonstration purposes. In
fact, you may encounter the following message if the departure rate is
too high relative to the average relational duration. In this test case
below, the average “lifespan” is half as long as the average
relationship (which probably doesn’t make any sense). We have tried to
catch this problem for you with an informative error message. Ok, so
let’s use our smaller d.rate parameter of 0.001.
coef.diss.high <- dissolution_coefs(dissolution = ~offset(edges),
duration = 40, d.rate = 0.05)
Estimation
The network model is estimated using the netest function
with all the inputs we specified above.
est1 <- netest(nw, formation, target.stats, coef.diss)
Diagnostics
For the diagnostics for this model, we set the
nwstats.formula to expand the formation formula to specify
that we want to monitor the mean degree and mixing by the
risk attribute. We do this with nodefactor and
nodematch terms, respectively. By adding them to the
nwstats.formula, but not in the formation formula for the
TERGM itself, we can get summary statistics for simulations to see what
the expected values of these terms would be in a null model. Setting
levels = NULL in the nodefactor term will
output statistics for both risk groups in the model. We can also monitor
the nodematch term with a diff = TRUE
argument, which allows for differential homophily by group. In this
model, there would never be a reason to specify differential homophily
by group in the ERGM formula because it would be overspecified
(individual diagonal cells are a function of edges and
nodefactor terms). It can be used for models either without
a nodefactor term, or for models with
nodefactor terms but with a mixing attribute with more than
two levels. But again we show it here for comparison, and getting you
familiar with the different syntax options.
dx1 <- netdx(est1, nsims = 10, nsteps = 1000, ncores = 4,
nwstats.formula = ~edges +
nodefactor("risk", levels = NULL) +
nodematch("risk", diff = TRUE))
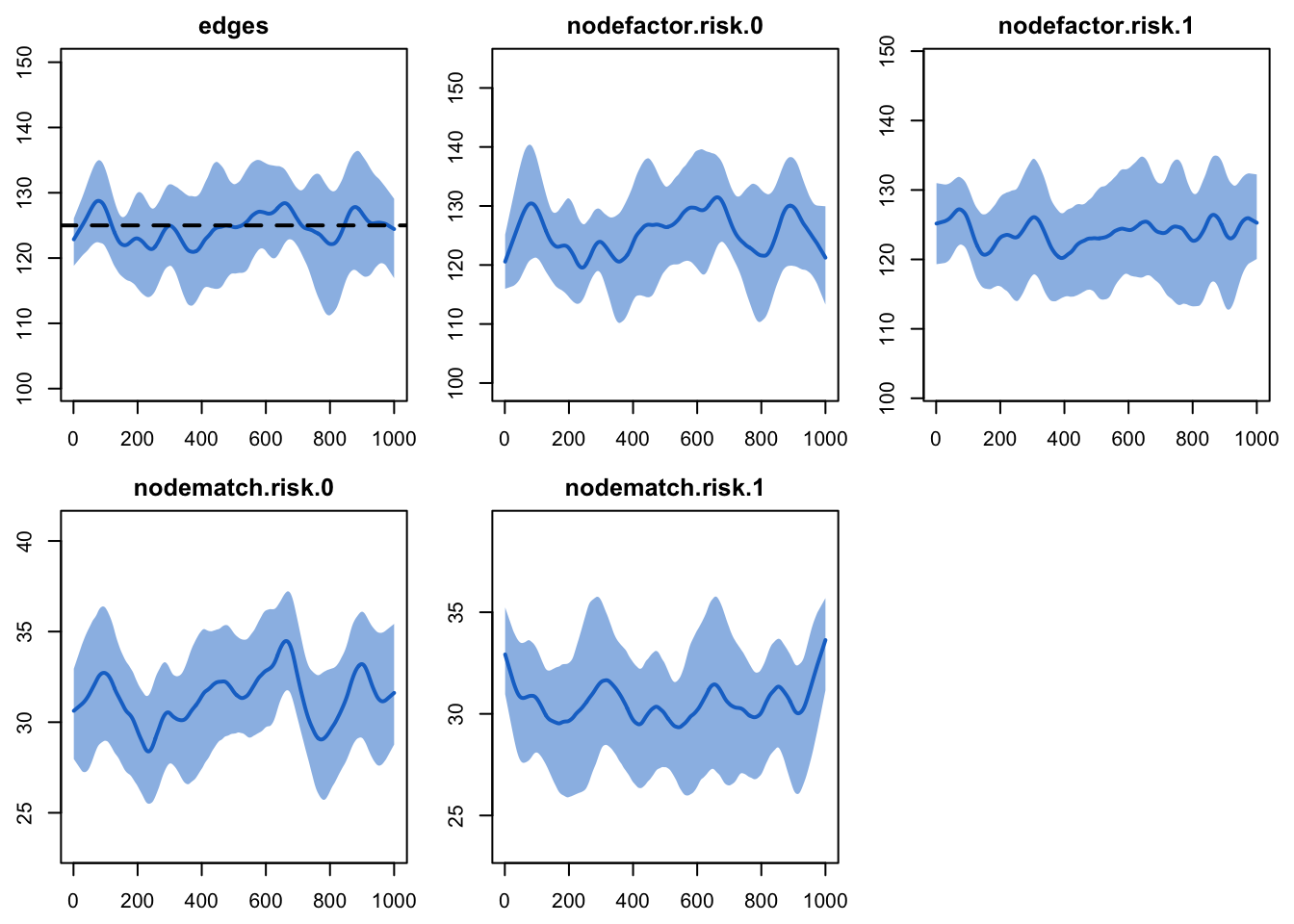
Printing the diagnostics shows a good fit between the targets and the
simulated outputs. There is no difference between the simulated means
for nodefactor statistics for risk group 0 compared to risk
group 1, indicating no differential in mean degree by risk group.
dx1
EpiModel Network Diagnostics
=======================
Diagnostic Method: Dynamic
Simulations: 10
Time Steps per Sim: 1000
Formation Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SD
edges 125 124.742 -0.206 11.362
nodefactor.risk.0 NA 125.555 NA 14.306
nodefactor.risk.1 NA 123.929 NA 13.095
nodematch.risk.0 NA 31.343 NA 5.444
nodematch.risk.1 NA 30.530 NA 5.494
Duration Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SD
edges 40 39.8 -0.501 1.021
Dissolution Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SD
edges 0.025 0.025 -0.065 0
Plotting the diagnostics shows that the simulations are right on
target for the terms in the formation model. We will skip plotting the
dissolution model diagnostics for this example.
plot(dx1)
Model 2: Assortative Mixing and Differential Degree
The counterfactual in Model 2 will add differentials in mean degree
by risk group and for homophily in risk group mixing by using
nodefactor and nodematch terms and associated
target statistics.
Parameterization
The formula for the formation component of the model will now be as
follows. The nodefactor term represents variation in the
overall mean degree by the named attribute, risk. The
nodematch represents mixing by that named attribute.
formation <- ~edges + nodefactor("risk") + nodematch("risk")
As noted, the overall mean degree will remain the same at 0.5 across
the two models, but the mean degree by risk group will differ. We will
specify that the mean degree for risk group 1 is 0.75. Because the
overall mean degree is 0.5, and the proportions of risk groups is equal,
that implies that the mean degree for risk group 0 will be 0.25. The
target statistic for the nodefactor term is the product of
the mean degree of risk group 1 and the size of risk group 1:
0.75 * 250 = 187.5. Finally, we will specify that 90% of
the partnerships occur between persons of the same risk group, which
equals 112.5 edges.
target.stats <- c(125, 187.5, 112.5)
The other components of the model, including the network object and
dissolution model components, are recycled from Model 1.
Estimation
The new target statistics are entered in this new model with the
remaining components from Model 1.
est2 <- netest(nw, formation, target.stats, coef.diss)
We can use the summary function to evaluate the
coefficient estimates for the nodefactor and
nodematch terms, which are strong and highly significant.
The specific values of those coefficients do not matter much here (what
matters is how they generate simulations of the complete network,
below), but the positive sign of both terms shows these are greater than
expected than under the null model, precisely as we have parameterized
them.
summary(est2)
Call:
ergm(formula = formation.nw, constraints = constraints, offset.coef = coef.form,
target.stats = target.stats, eval.loglik = FALSE, control = set.control.ergm,
verbose = verbose)
Monte Carlo Maximum Likelihood Results:
Estimate Std. Error MCMC % z value Pr(>|z|)
edges -9.1328 0.3034 0 -30.106 <1e-04 ***
nodefactor.risk.1 0.6278 0.1145 0 5.482 <1e-04 ***
nodematch.risk 2.0069 0.3002 0 6.684 <1e-04 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Log-likelihood was not estimated for this fit. To get deviances, AIC, and/or BIC, use ‘*fit* <-logLik(*fit*, add=TRUE)’ to add it to the object or rerun this function with eval.loglik=TRUE.
Dissolution Coefficients
=======================
Dissolution Model: ~offset(edges)
Target Statistics: 40
Crude Coefficient: 3.663562
Mortality/Exit Rate: 0.001
Adjusted Coefficient: 3.7469
Diagnostics
The diagnostics on this second model are run using the same approach
as Model 1, but we pass in the fitted model object for Model 2.
dx2 <- netdx(est2, nsims = 10, nsteps = 1000, ncores = 4,
nwstats.formula = ~edges +
nodefactor("risk", levels = NULL) +
nodematch("risk", diff = TRUE))
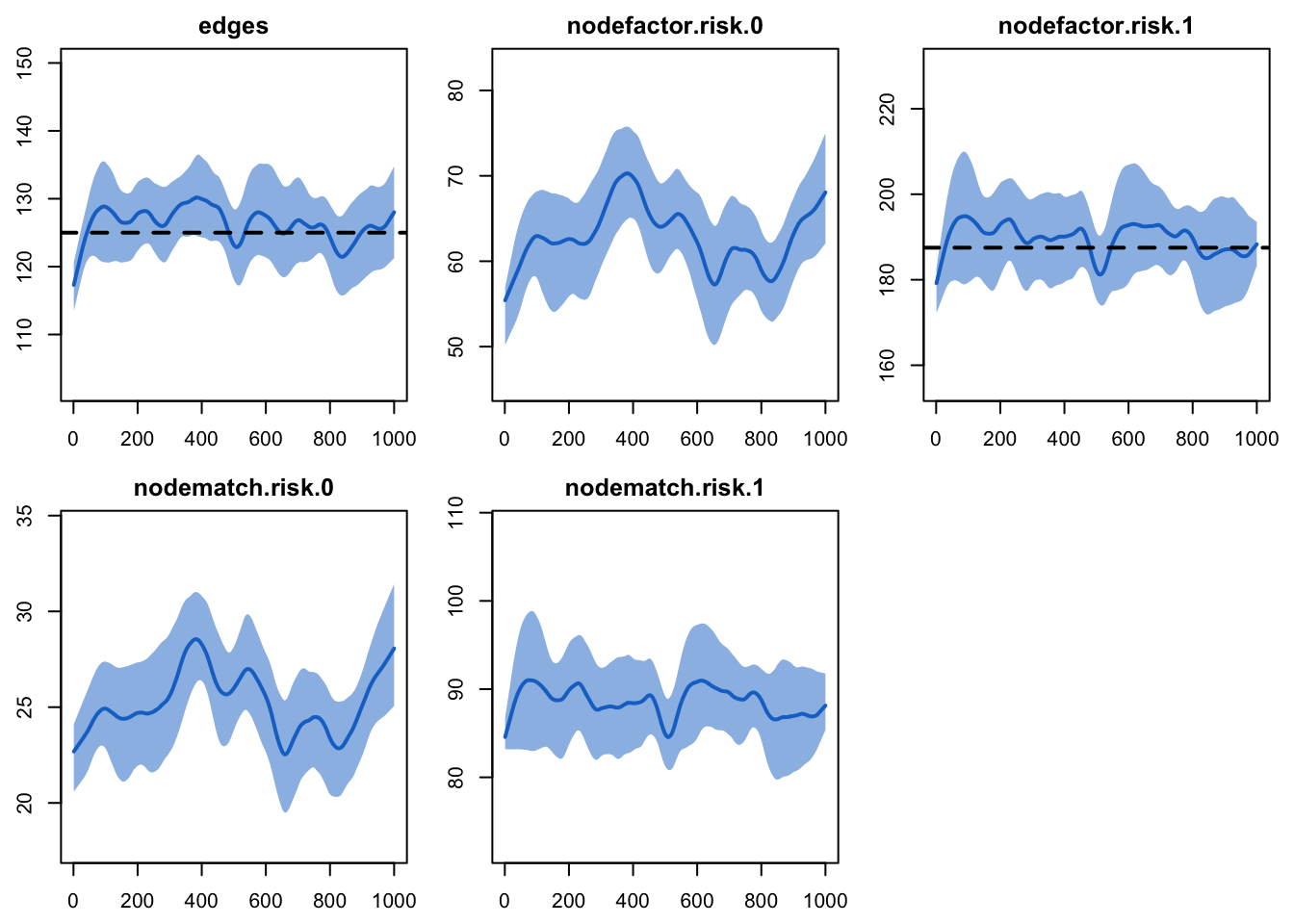
Printing the model shows that the simulated network statistics are
consistent with the target statistics in the formation and dissolution
model. The simulated mean for the nodefactor target
statistic for risk group 0 corresponds to a mean degree of 0.25 (more
exactly: 62.9432 / 250 = 0.2517728) in that group, as expected.
dx2
EpiModel Network Diagnostics
=======================
Diagnostic Method: Dynamic
Simulations: 10
Time Steps per Sim: 1000
Formation Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SD
edges 125.0 126.354 1.083 9.986
nodefactor.risk.0 NA 62.943 NA 10.108
nodefactor.risk.1 187.5 189.765 1.208 17.832
nodematch.risk.0 NA 25.198 NA 4.639
nodematch.risk.1 NA 88.608 NA 8.967
nodematch.risk 112.5 NA NA NA
Duration Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SD
edges 40 40.173 0.434 0.713
Dissolution Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SD
edges 0.025 0.025 -0.193 0
The plots look fine here, so we move onto the epidemic
simulation.
plot(dx2)
Epidemic Simulation
This epidemic simulation will investigate how variation in mean
degree by risk group and highly assortative risk group mixing jointly
impact epidemic prevalence overall and by risk group. We will use one
set of epidemic parameters, initial conditions, and control settings
shared across the two counterfactual models.
Parameterization
The parameters are entered into the param.net function
as in previous tutorial. Since this is an SI epidemic, there will be no
recovery rate parameter. The three new parameters will control the
arrival rate, departure rate among the susceptibles, and departure rate
in the infected group. Note that this is the same rate as what we
specified in dissolution_coefs. For this tutorial, we will
assume that all three rates are equal, which implies that there is no
disease-induced mortality and a stable population size. These can be
experimented with in the next lab.
param <- param.net(inf.prob = 0.1, act.rate = 5,
a.rate = 0.001, ds.rate = 0.001, di.rate = 0.001)
Similar to the previous tutorial, we only need to specify the number
infected at the outset. To generate stable epidemic conditions quickly,
we will see that the prevalence is 10%, distributed randomly among the
population.
init <- init.net(i.num = 50)
The inputs for the control settings share some similarities with the
control settings from the Day 3 tutorials, but we will be adding some
new parameters here:
resimulate.network: this argument specifies that the
network should be resimulated timestep-by-timestep in the model, in
response to changing conditions like demography. By default this
argument is FALSE, so here we must set it to
TRUE.epi.by: this argument provides stratified prevalence
estimates by a categorical attribute in the network (if we had used the
special group attribute, stratified estimates would be
available by group by default). By default, this argument is
NULL.tergmLite: this is a streamlined approach for network
simulation that speeds up the process by 20-50 fold. This is possible
because of trade offs between complete versus sparse representation of
the underlying network object. By default this is set to
FALSE, which means that the full network object is
retained. With tergmLite methods, this means that the full network
object cannot be plotted at different time points (because the
individual-level network history is not retained). Otherwise, the two
methods should be equivalent.
tergmLite Comparison
For the sake of comparing simulation efficiency with and without
tergmLite, let’s run a single simulation of Model 1 with each method.
All that needs to be changed is the tergmLite
parameter.
control.full <- control.net(type = "SI", nsteps = 300, nsims = 1, ncores = 1,
resimulate.network = TRUE, epi.by = "risk", tergmLite = FALSE)
control.tl <- control.net(type = "SI", nsteps = 300, nsims = 1, ncores = 1,
resimulate.network = TRUE, epi.by = "risk", tergmLite = TRUE)
Next, we will run a single simulation here live, so you can compare
the speed difference.
sim1.full <- netsim(est1, param, init, control.full)
sim1.tl <- netsim(est1, param, init, control.tl)
And with the difference in speed comes the trade off with the data
calculated and stored. In the full (non-tergmLite) version, we retain
the contact network data:
sim1.full
EpiModel Simulation
=======================
Model class: netsim
Simulation Summary
-----------------------
Model type: SI
No. simulations: 1
No. time steps: 300
No. NW groups: 1
Fixed Parameters
---------------------------
inf.prob = 0.1
act.rate = 5
a.rate = 0.001
ds.rate = 0.001
di.rate = 0.001
groups = 1
Model Output
-----------------------
Variables: s.num s.num.risk0 s.num.risk1 i.num i.num.risk0
i.num.risk1 num num.risk0 num.risk1 si.flow ds.flow di.flow
a.flow
Networks: sim1
Transmissions: sim1
Formation Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SD
edges 125 141.747 13.397 11.029
Dissolution Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SD
edges 0.025 NaN NaN NA
And in the tergmLite version, we do not. We still have access to all
the data except for the network history, which is typically not needed
for full-scale research models anyway.
sim1.tl
EpiModel Simulation
=======================
Model class: netsim
Simulation Summary
-----------------------
Model type: SI
No. simulations: 1
No. time steps: 300
No. NW groups: 1
Fixed Parameters
---------------------------
inf.prob = 0.1
act.rate = 5
a.rate = 0.001
ds.rate = 0.001
di.rate = 0.001
groups = 1
Model Output
-----------------------
Variables: s.num s.num.risk0 s.num.risk1 i.num i.num.risk0
i.num.risk1 num num.risk0 num.risk1 si.flow ds.flow di.flow
a.flow
Transmissions: sim1
Formation Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SD
edges 125 121.53 -2.776 6.96
Dissolution Diagnostics
-----------------------
Not available when:
- `control$tergmLite == TRUE`
- `control$save.network == FALSE`
- dissolution formula is not `~ offset(edges)`
Main Epidemic Simulation
For the main epidemic model comparison, we are going to run 5
simulations on 5 cores with tergmLite = TRUE. Each model
run takes about in about 45 seconds on my laptop.
control <- control.net(type = "SI", nsteps = 300, nsims = 5, ncores = 5,
resimulate.network = TRUE, epi.by = "risk", tergmLite = TRUE)
To simulate the two network models, we use two calls to the
netsim function, one with the fitted estimation object from
Model 1 and the other from Model 2. When run in interactive mode, basic
output from the model progress will be printed to the console, with
information on current prevalence, population size, and flows.
sim1 <- netsim(est1, param, init, control)
sim2 <- netsim(est2, param, init, control)
Printing the netsim output object shows its contents.
The output compartments now include both the overall susceptible and
infected numbers but also the numbers stratified by values of the risk
group variable.
sim1
EpiModel Simulation
=======================
Model class: netsim
Simulation Summary
-----------------------
Model type: SI
No. simulations: 5
No. time steps: 300
No. NW groups: 1
Fixed Parameters
---------------------------
inf.prob = 0.1
act.rate = 5
a.rate = 0.001
ds.rate = 0.001
di.rate = 0.001
groups = 1
Model Output
-----------------------
Variables: s.num s.num.risk0 s.num.risk1 i.num i.num.risk0
i.num.risk1 num num.risk0 num.risk1 si.flow ds.flow di.flow
a.flow
Transmissions: sim1 ... sim5
Formation Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SD
edges 125 120.899 -3.281 13.686
Dissolution Diagnostics
-----------------------
Not available when:
- `control$tergmLite == TRUE`
- `control$save.network == FALSE`
- dissolution formula is not `~ offset(edges)`
Model Analysis
Our model analysis will consist of model diagnostics, and then the
examination of the epidemiological outcomes overall and by risk
group.
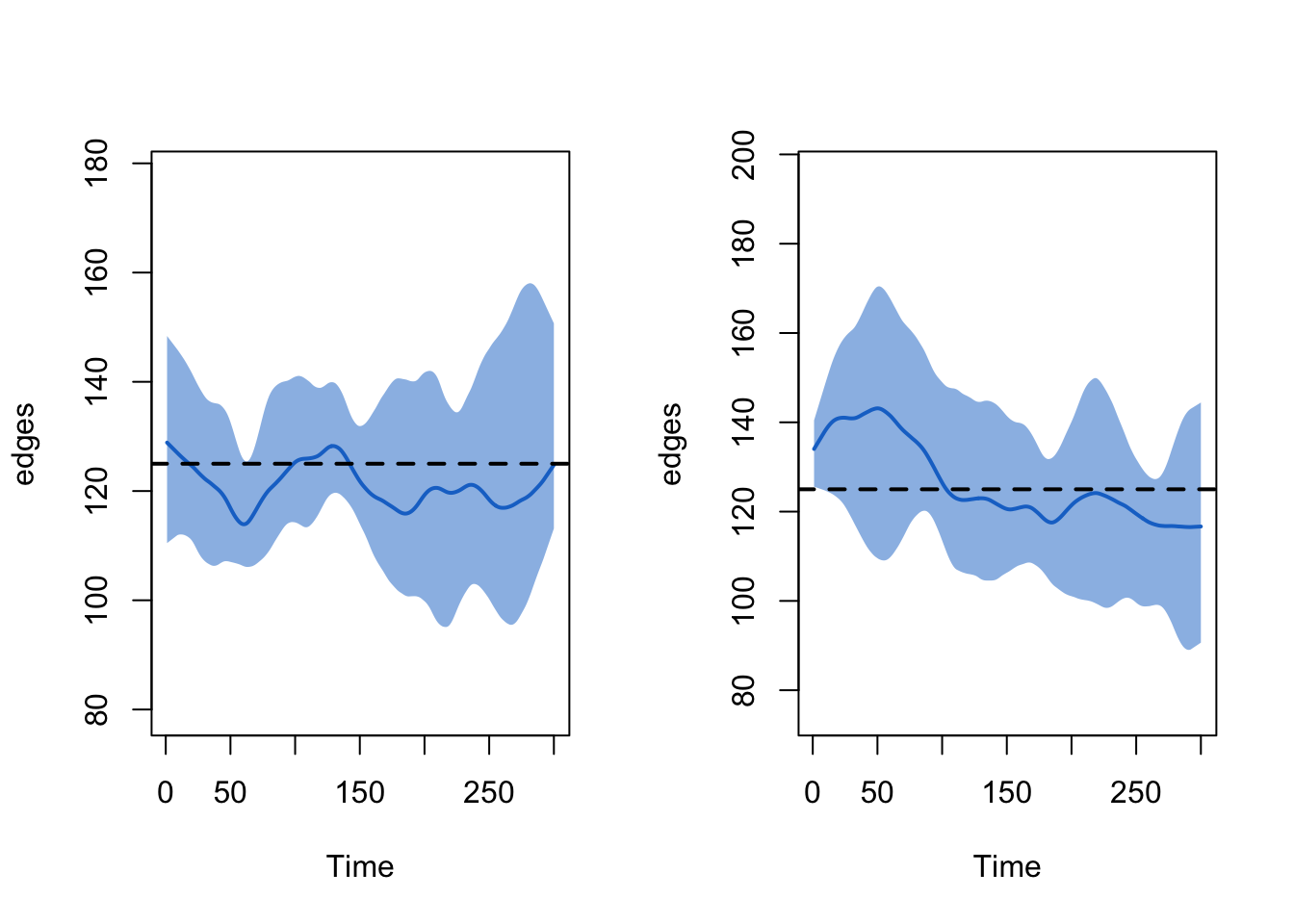
Post-Simulation Diagnostics
It is important to first examine the network model diagnostics after
the epidemic simulation, since the vital dynamics within these
simulations may have changed the structure of the network in unexpected
ways. Here we show how to plot model diagnostics recorded within the
epidemic simulation. Although we have saved all the network statistics
in the formation formula, here we plot the number of edges over
time.
par(mfrow = c(1, 2))
plot(sim1, type = "formation", stats = "edges", ylim = c(0, 250), qnts = 1)
plot(sim2, type = "formation", stats = "edges", ylim = c(0, 250), qnts = 1)
Epidemiologic Outcomes
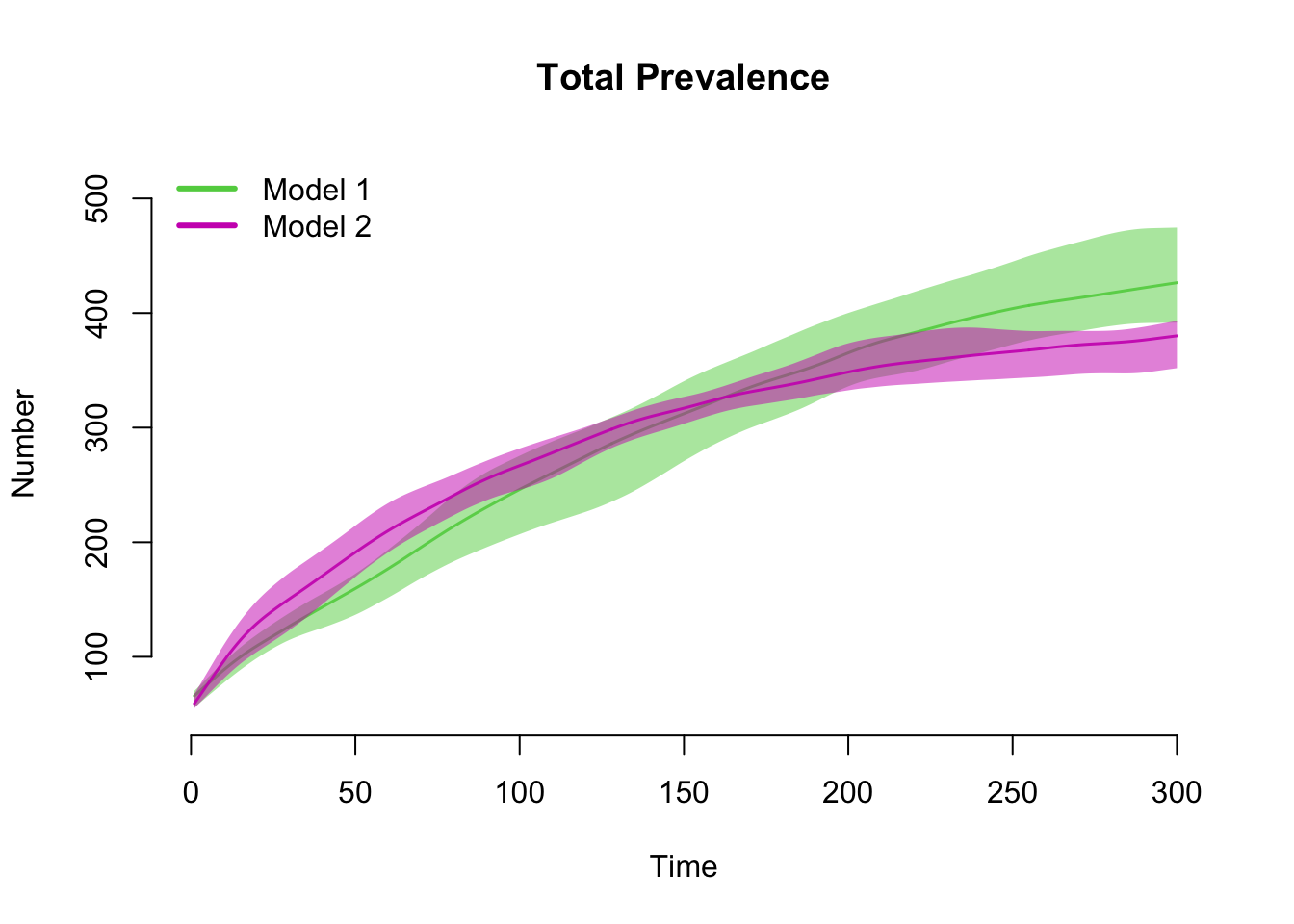
This example shows how to plot outputs of two separate simulation
objects onto one plot window using the add argument. Note
that this requires manual specification of the plot legend. Our
substantive result from this model comparison is that the total
prevalence in the population is about the same (not exactly, but pretty
close!).
par(mfrow = c(1, 1))
plot(sim1, y = "i.num", qnts = 1, main = "Total Prevalence", mean.col = 3, qnts.col = 3)
plot(sim2, y = "i.num", qnts = 1, mean.col = 6, qnts.col = 6, add = TRUE)
legend("topleft", c("Model 1", "Model 2"), lwd = 3, col = c(3, 6), bty = "n")
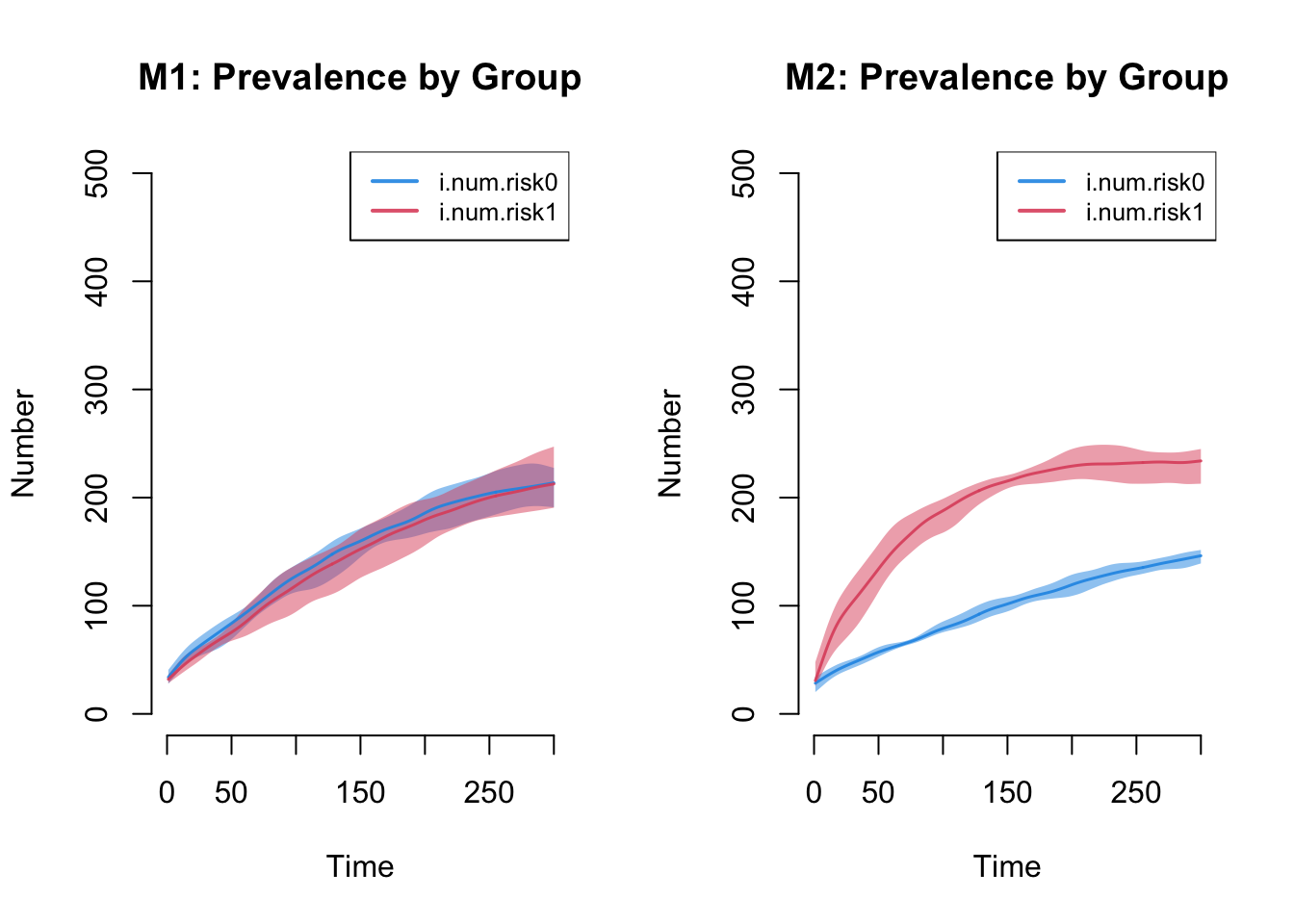
The next plot shows the prevalence by risk group in Model 1 compared
to Model 2. Setting the ylim manually is necessary to
ensure that the axes on both plots match. The substantive result is that
Model 1 shows no differences in prevalence by risk group (as expected)
and Model 2 shows large differences.
par(mfrow = c(1, 2))
plot(sim1, y = c("i.num.risk0", "i.num.risk1"), legend = TRUE, qnts = 1,
ylim = c(0, 500), main = "M1: Prevalence by Group")
plot(sim2, y = c("i.num.risk0", "i.num.risk1"), legend = TRUE, qnts = 1,
ylim = c(0, 500), main = "M2: Prevalence by Group")
Last updated: 2022-07-07 with EpiModel v2.3.0




