Tutorial: Adding An Asymptomatic Pathway and Screening-Based Interventions to the COVID Model
Day 5 | Network Modeling for Epidemics
In this tutorial, we will build on our COVID-19 model by adding a more complex disease progression structure, with clinical versus sub-clinical (asymptomatic) pathways, as well as disease screening and diagnosis-based interventions.
Setup
First start by loading EpiModel and clearing your global environment.
library(EpiModel)
rm(list = ls())We will use the network model parameterization and extension functions from the previous tutorial as the starting point for this tutorial.
Network Initialization
The network will have the same age and aging structure as the previous model. We have to reinitialize the mortality rates as in the last model.
ages <- 0:85
departure_rate <- c(588.45, 24.8, 11.7, 14.55, 47.85, 88.2, 105.65, 127.2,
154.3, 206.5, 309.3, 495.1, 736.85, 1051.15, 1483.45,
2294.15, 3642.95, 6139.4, 13938.3)
dr_pp_pd <- departure_rate / 1e5 / 365
age_spans <- c(1, 4, rep(5, 16), 1)
dr_vec <- rep(dr_pp_pd, times = age_spans)The network size and age attribute are next added.
n <- 1000
nw <- network_initialize(n)
ageVec <- sample(ages, n, replace = TRUE)
nw <- set_vertex_attribute(nw, "age", ageVec)We will also initialize the status vector as in the past
model, plus add three new nodal attributes that are needed for the new
extension epidemic models. statusTime will track when a
node changes disease stage; it is initialized as NA for
everyone and then set to time step 1 for those who are infected.
clinical will be a binary attribute to record whether nodes
are in a clinical or subclinical pathway; this will be initialized as
NA for everyone because it is updated at the move of
transition out of the latent (E) state. Finally, dxStatus
will keep track of the diagnosed nodal status; it will have three values
(0 for never screened, 1 for screened
negative, and 2 for screened positive), but everyone will
be initialized as 0. As with the others, all nodal attributes are set on
the network object with set_vertex_attribute.
statusVec <- rep("s", n)
init.latent <- sample(1:n, 50)
statusVec[init.latent] <- "e"
statusTime <- rep(NA, n)
statusTime[which(statusVec == "e")] <- 1
clinical <- rep(NA, n)
dxStatus <- rep(0, n)
nw <- set_vertex_attribute(nw, "status", statusVec)
nw <- set_vertex_attribute(nw, "statusTime", statusTime)
nw <- set_vertex_attribute(nw, "clinical", clinical)
nw <- set_vertex_attribute(nw, "dxStatus", dxStatus)
nw Network attributes:
vertices = 1000
directed = FALSE
hyper = FALSE
loops = FALSE
multiple = FALSE
bipartite = FALSE
total edges= 0
missing edges= 0
non-missing edges= 0
Vertex attribute names:
age clinical dxStatus status statusTime vertex.names
No edge attributesNew Modules
The new epidemic modules will involve some minor and major updates to our extension modules from the previous tutorial, and the addition of a new module to handle COVID screening and diagnosis.
Progression
The more sophisticated progression module that we develop below corresponds to this flow diagram, which is an extension of the SEIR diagram. Here, persons who are infected enter one of two pathways: a clinical (symptomatic) pathway and a sub-clinical (asymptomatic) pathway. This follows emerging research suggesting that a substantial fraction of COVID cases never experience any symptoms yet still transmit (although likely at a lower rate). In the clinical pathway, persons are further subdivided into a pre-symptomatic and symptomatic phase to reflect that infectiousness may occur just prior to symptoms.
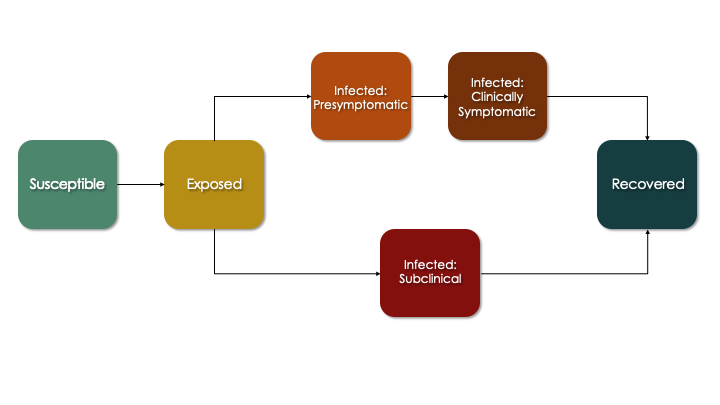
In the updated progression function below, we build out in code what is shown in the figure above. Each transition from one state to another involves a random Bernoulli process with the probability equal to the transition rate (which is the reciprocal of the average time spent in the current state before transition).
To determine how people enter the subclinical versus clinical
pathway, we will use the prop.clinical parameter, which is
actually a vector of probabilities corresponding to decade of age. This
will allow the level of asymptomatic infection to decrease over age, as
evidence suggests. The age.group calculation involves
rounding down the continous age in years to a decade, which is then used
to index the prop.clinical vector. The
clinical attribute is then assigned and stays with each
person throughout their infection.
Note that we also include a feature here of tracking the individual
statusTime, which is the time step of transition from one
state to another. This allows us to prevent immediate transitions across
multiple states within a single time step, since the condition for
transition requires statusTime < at.
progress2 <- function(dat, at) {
## Attributes
active <- get_attr(dat, "active")
status <- get_attr(dat, "status")
age <- get_attr(dat, "age")
statusTime <- get_attr(dat, "statusTime")
clinical <- get_attr(dat, "clinical")
## Parameters
prop.clinical <- get_param(dat, "prop.clinical")
ea.rate <- get_param(dat, "ea.rate")
ar.rate <- get_param(dat, "ar.rate")
eip.rate <- get_param(dat, "eip.rate")
ipic.rate <- get_param(dat, "ipic.rate")
icr.rate <- get_param(dat, "icr.rate")
## Determine Subclinical (E to A) or Clinical (E to Ip to Ic) pathway
ids.newInf <- which(active == 1 & status == "e" & statusTime <= at & is.na(clinical))
num.newInf <- length(ids.newInf)
if (num.newInf > 0) {
age.group <- pmin((floor(age[ids.newInf] / 10)) + 1, 8)
prop.clin.vec <- prop.clinical[age.group]
if (any(is.na(prop.clin.vec))) stop("error in prop.clin.vec")
vec.new.clinical <- rbinom(num.newInf, 1, prop.clin.vec)
clinical[ids.newInf] <- vec.new.clinical
}
## Subclinical Pathway
# E to A: latent move to asymptomatic infectious
num.new.EtoA <- 0
ids.Es <- which(active == 1 & status == "e" & statusTime < at & clinical == 0)
num.Es <- length(ids.Es)
if (num.Es > 0) {
vec.new.A <- which(rbinom(num.Es, 1, ea.rate) == 1)
if (length(vec.new.A) > 0) {
ids.new.A <- ids.Es[vec.new.A]
num.new.EtoA <- length(ids.new.A)
status[ids.new.A] <- "a"
statusTime[ids.new.A] <- at
}
}
# A to R: asymptomatic infectious move to recovered
num.new.AtoR <- 0
ids.A <- which(active == 1 & status == "a" & statusTime < at & clinical == 0)
num.A <- length(ids.A)
if (num.A > 0) {
vec.new.R <- which(rbinom(num.A, 1, ar.rate) == 1)
if (length(vec.new.R) > 0) {
ids.new.R <- ids.A[vec.new.R]
num.new.AtoR <- length(ids.new.R)
status[ids.new.R] <- "r"
statusTime[ids.new.R] <- at
}
}
## Clinical Pathway
# E to Ip: latent move to preclinical infectious
num.new.EtoIp <- 0
ids.Ec <- which(active == 1 & status == "e" & statusTime < at & clinical == 1)
num.Ec <- length(ids.Ec)
if (num.Ec > 0) {
vec.new.Ip <- which(rbinom(num.Ec, 1, eip.rate) == 1)
if (length(vec.new.Ip) > 0) {
ids.new.Ip <- ids.Ec[vec.new.Ip]
num.new.EtoIp <- length(ids.new.Ip)
status[ids.new.Ip] <- "ip"
statusTime[ids.new.Ip] <- at
}
}
# Ip to Ic: preclinical infectious move to clinical infectious
num.new.IptoIc <- 0
ids.Ip <- which(active == 1 & status == "ip" & statusTime < at & clinical == 1)
num.Ip <- length(ids.Ip)
if (num.Ip > 0) {
vec.new.Ic <- which(rbinom(num.Ip, 1, ipic.rate) == 1)
if (length(vec.new.Ic) > 0) {
ids.new.Ic <- ids.Ip[vec.new.Ic]
num.new.IptoIc <- length(ids.new.Ic)
status[ids.new.Ic] <- "ic"
statusTime[ids.new.Ic] <- at
}
}
# Ic to R: clinical infectious move to recovered (if not mortality first)
num.new.IctoR <- 0
ids.Ic <- which(active == 1 & status == "ic" & statusTime < at & clinical == 1)
num.Ic <- length(ids.Ic)
if (num.Ic > 0) {
vec.new.R <- which(rbinom(num.Ic, 1, icr.rate) == 1)
if (length(vec.new.R) > 0) {
ids.new.R <- ids.Ic[vec.new.R]
num.new.IctoR <- length(ids.new.R)
status[ids.new.R] <- "r"
statusTime[ids.new.R] <- at
}
}
## Save updated status attribute
dat <- set_attr(dat, "status", status)
dat <- set_attr(dat, "statusTime", statusTime)
dat <- set_attr(dat, "clinical", clinical)
## Save summary statistics
dat <- set_epi(dat, "ea.flow", at, num.new.EtoA)
dat <- set_epi(dat, "ar.flow", at, num.new.AtoR)
dat <- set_epi(dat, "eip.flow", at, num.new.EtoIp)
dat <- set_epi(dat, "ipic.flow", at, num.new.IptoIc)
dat <- set_epi(dat, "icr.flow", at, num.new.IctoR)
dat <- set_epi(dat, "e.num", at, sum(status == "e"))
dat <- set_epi(dat, "a.num", at, sum(status == "a"))
dat <- set_epi(dat, "ip.num", at, sum(status == "ip"))
dat <- set_epi(dat, "ic.num", at, sum(status == "ic"))
dat <- set_epi(dat, "r.num", at, sum(status == "r"))
return(dat)
}At the end of the function, we reset the relevant attributes that
have changed on the dat object and keep track of all the
flow sizes and state sizes. There are several more flows and states to
track now, compared to the earlier SEIR model!
Diagnosis
The diagnosis module will handle the process for screening of cases,
which here is controlled by two screening rate parameters,
dx.rate.sympt and dx.rate.other. The former
parameter controls the rate of screening for persons currently with
symptomatic infection (that is, in the ic disease state),
while the latter parameter controls the rate for all other persons. This
reflects the higher rates of symptoms-based diagnosis of active
cases.
Additionally, we have a logical parameter,
allow.rescreen, that controls whether persons who have
previously had a negative COVID test can subsequently retest (this is
why we wanted to track dxStatus as a three-level variables
of never-tested, tested-negative, and tested-positive). Finally, because
COVID diagnostics are imperfect, we incorporate PCR sensitive parameter,
pcr.sens, to simulate the process of false-negative test
results.
dx_covid <- function(dat, at) {
## Pull attributes
active <- get_attr(dat, "active")
status <- get_attr(dat, "status")
dxStatus <- get_attr(dat, "dxStatus")
## Pull parameters
dx.rate.sympt <- get_param(dat, "dx.rate.sympt")
dx.rate.other <- get_param(dat, "dx.rate.other")
allow.rescreen <- get_param(dat, "allow.rescreen")
pcr.sens <- get_param(dat, "pcr.sens")
## Initialize trackers
idsDx.sympt <- idsDx.other <- NULL
idsDx.sympt.pos <- idsDx.other.pos.true <- NULL
idsDx.sympt.neg <- idsDx.other.pos.false <- NULL
## Determine screening eligibility
idsElig.sympt <- which(active == 1 & dxStatus %in% 0:1 & status == "ic")
if (allow.rescreen == TRUE) {
idsElig.other <- which(active == 1 & dxStatus %in% 0:1 &
status %in% c("s", "e", "a", "ip", "r"))
} else {
idsElig.other <- which(active == 1 & dxStatus == 0 &
status %in% c("s", "e", "a", "ip", "r"))
}
## Symptomatic testing
nElig.sympt <- length(idsElig.sympt)
if (nElig.sympt > 0) {
vecDx.sympt <- which(rbinom(nElig.sympt, 1, dx.rate.sympt) == 1)
idsDx.sympt <- idsElig.sympt[vecDx.sympt]
nDx.sympt <- length(idsDx.sympt)
if (nDx.sympt > 0) {
vecDx.sympt.pos <- rbinom(nDx.sympt, 1, pcr.sens)
idsDx.sympt.pos <- idsDx.sympt[which(vecDx.sympt.pos == 1)]
idsDx.sympt.neg <- idsDx.sympt[which(vecDx.sympt.pos == 0)]
dxStatus[idsDx.sympt.pos] <- 2
dxStatus[idsDx.sympt.neg] <- 1
}
}
## Asymptomatic screening
nElig.other <- length(idsElig.other)
if (nElig.other > 0) {
vecDx.other <- which(rbinom(nElig.other, 1, dx.rate.other) == 1)
idsDx.other <- idsElig.other[vecDx.other]
nDx.other <- length(idsDx.other)
if (nDx.other > 0) {
idsDx.other.neg <- intersect(idsDx.other, which(status == "s"))
idsDx.other.pos.all <- intersect(idsDx.other,
which(status %in% c("e", "a", "ip", "r")))
vecDx.other.pos <- rbinom(length(idsDx.other.pos.all), 1, pcr.sens)
idsDx.other.pos.true <- idsDx.other.pos.all[which(vecDx.other.pos == 1)]
idsDx.other.pos.false <- idsDx.other.pos.all[which(vecDx.other.pos == 0)]
dxStatus[idsDx.other.neg] <- 1
dxStatus[idsDx.other.pos.false] <- 1
dxStatus[idsDx.other.pos.true] <- 2
}
}
## Set attr
dat <- set_attr(dat, "dxStatus", dxStatus)
## Summary statistics
dat <- set_epi(dat, "nDx", at, length(idsDx.sympt) + length(idsDx.other))
dat <- set_epi(dat, "nDx.pos", at, length(idsDx.sympt.pos) +
length(idsDx.other.pos.true))
dat <- set_epi(dat, "nDx.pos.sympt", at, length(idsDx.sympt.pos))
dat <- set_epi(dat, "nDx.pos.fn", at, length(idsDx.sympt.neg) +
length(idsDx.other.pos.false))
return(dat)
}At the end of the function, we updated the modified
dxStatus attribute, and calculate some summary statistics
for new cases.
Infection
It is also necessary to update the infection module function in a couple of ways. The first will reflect that we now have 3 infectious disease states, of varying infectiousness, compared to the earlier SEIR model’s one infectious state. This requires modifying the code querying the definition of infectious nodes, and the construction of the discordant edgelist.
Second, onto the discordant edgelist data frame, we add the disease
state of the infectious node and the diagnostic status of that node.
Those new data are then used in two ways. First, being in the
asymptomatic disease state, a, is associated with a lower
probability of transmission compared to the other two (clinical)
infectious disease states. That is accomplished by modifying the base
transmission probability by a relative risk parameter,
inf.prob.a.rr.
Second, being infectious and diagnosed positive (which a
dxState of 2), may trigger behavioral interventions reflect
case isolation. This type of behavioral change may be accomplished in
several different ways. Here it involves a modification of the
act.rate parameter that controls the number of individual
exposure events between active dyads in the current time step. This type
of intervention may start at a particular time step,
act.rate.dx.inter.time, and result in a relative reduction
in the current act rate of act.rate.dx.inter.rr.
infect2 <- function(dat, at) {
## Uncomment this to run environment interactively
# browser()
## Attributes ##
active <- get_attr(dat, "active")
status <- get_attr(dat, "status")
infTime <- get_attr(dat, "infTime")
dxStatus <- get_attr(dat, "dxStatus")
statusTime <- get_attr(dat, "statusTime")
## Parameters ##
inf.prob <- get_param(dat, "inf.prob")
act.rate <- get_param(dat, "act.rate")
inf.prob.a.rr <- get_param(dat, "inf.prob.a.rr")
act.rate.dx.inter.time <- get_param(dat, "act.rate.dx.inter.time")
act.rate.dx.inter.rr <- get_param(dat, "act.rate.dx.inter.rr")
## Find infected nodes ##
infstat <- c("a", "ic", "ip")
idsInf <- which(active == 1 & status %in% infstat)
nActive <- sum(active == 1)
nElig <- length(idsInf)
## Initialize default incidence at 0 ##
nInf <- 0
## If any infected nodes, proceed with transmission ##
if (nElig > 0 && nElig < nActive) {
## Look up discordant edgelist ##
del <- discord_edgelist(dat, at, infstat = infstat)
## If any discordant pairs, proceed ##
if (!(is.null(del))) {
del$status <- status[del$inf]
del$dxStatus <- dxStatus[del$inf]
# Set parameters on discordant edgelist data frame
del$transProb <- inf.prob
del$transProb[del$status == "a"] <- del$transProb[del$status == "a"] *
inf.prob.a.rr
del$actRate <- act.rate
if (at >= act.rate.dx.inter.time) {
del$actRate[del$dxStatus == 2] <- del$actRate[del$dxStatus == 2] *
act.rate.dx.inter.rr
}
del$finalProb <- 1 - (1 - del$transProb)^del$actRate
# Stochastic transmission process
transmit <- rbinom(nrow(del), 1, del$finalProb)
# Keep rows where transmission occurred
del <- del[which(transmit == 1), ]
# Look up new ids if any transmissions occurred
idsNewInf <- unique(del$sus)
nInf <- length(idsNewInf)
# Set new attributes and transmission matrix
if (nInf > 0) {
status[idsNewInf] <- "e"
infTime[idsNewInf] <- at
statusTime[idsNewInf] <- at
dat <- set_transmat(dat, del, at)
}
}
}
dat <- set_attr(dat, "status", status)
dat <- set_attr(dat, "infTime", infTime)
dat <- set_attr(dat, "statusTime", statusTime)
## Save summary statistics
dat <- set_epi(dat, "se.flow", at, nInf)
return(dat)
}There are no other modifications of the infection module other than
to track the statusTime upon infection and then resetting
that attribute on the dat object.
Births
The birth module requires a very minor change to update the three new
nodal attributes on the dat object for any incoming
nodes.
afunc2 <- function(dat, at) {
## Parameters ##
n <- get_epi(dat, "num", at - 1)
a.rate <- get_param(dat, "arrival.rate")
## Process ##
nArrivalsExp <- n * a.rate
nArrivals <- rpois(1, nArrivalsExp)
# Update attributes
if (nArrivals > 0) {
dat <- append_core_attr(dat, at = at, n.new = nArrivals)
dat <- append_attr(dat, "status", "s", nArrivals)
dat <- append_attr(dat, "infTime", NA, nArrivals)
dat <- append_attr(dat, "age", 0, nArrivals)
dat <- append_attr(dat, "statusTime", NA, nArrivals)
dat <- append_attr(dat, "clinical", NA, nArrivals)
dat <- append_attr(dat, "dxStatus", 0, nArrivals)
}
## Summary statistics ##
dat <- set_epi(dat, "a.flow", at, nArrivals)
return(dat)
}Deaths
The death module requires an even more minor modification from the
last tutorial, which involves simulating COVID-related mortality and
tracking the number of covid.deaths based on deaths that
occurs within the ic (clinical symptomatic) state
(previously these were in the i state only).
dfunc2 <- function(dat, at) {
## Attributes
active <- get_attr(dat, "active")
exitTime <- get_attr(dat, "exitTime")
age <- get_attr(dat, "age")
status <- get_attr(dat, "status")
## Parameters
dep.rates <- get_param(dat, "departure.rates")
dep.dis.mult <- get_param(dat, "departure.disease.mult")
## Query alive
idsElig <- which(active == 1)
nElig <- length(idsElig)
## Initialize trackers
nDepts <- 0
idsDepts <- NULL
if (nElig > 0) {
## Calculate age-specific departure rates for each eligible node ##
## Everyone older than 85 gets the final mortality rate
whole_ages_of_elig <- pmin(ceiling(age[idsElig]), 86)
departure_rates_of_elig <- dep.rates[whole_ages_of_elig]
## Multiply departure rates for diseased persons
idsElig.inf <- which(status[idsElig] == "ic")
departure_rates_of_elig[idsElig.inf] <- departure_rates_of_elig[idsElig.inf] * dep.dis.mult
## Simulate departure process
vecDepts <- which(rbinom(nElig, 1, departure_rates_of_elig) == 1)
idsDepts <- idsElig[vecDepts]
nDepts <- length(idsDepts)
## Update nodal attributes
if (nDepts > 0) {
active[idsDepts] <- 0
exitTime[idsDepts] <- at
}
}
## Reset attributes
dat <- set_attr(dat, "active", active)
dat <- set_attr(dat, "exitTime", exitTime)
## Summary statistics ##
dat <- set_epi(dat, "total.deaths", at, nDepts)
# covid deaths
covid.deaths <- length(intersect(idsDepts, which(status == "ic")))
dat <- set_epi(dat, "covid.deaths", at, covid.deaths)
return(dat)
}Network Model Estimation
With epidemic modules designed, we parameterize the exact same network model as the previous tutorial.
formation <- ~edges + degree(0) + absdiff("age")
mean_degree <- 2
edges <- mean_degree * (n/2)
avg.abs.age.diff <- 2
isolates <- n * 0.08
absdiff <- edges * avg.abs.age.diff
target.stats <- c(edges, isolates, absdiff)
target.stats[1] 1000 80 2000coef.diss <- dissolution_coefs(~offset(edges), 20, mean(dr_vec))
coef.dissDissolution Coefficients
=======================
Dissolution Model: ~offset(edges)
Target Statistics: 20
Crude Coefficient: 2.944439
Mortality/Exit Rate: 3.159205e-05
Adjusted Coefficient: 2.945703We estimate the model with netest. Here we demonstrate
how to increase the maximum number of MCMLE iterations (the default is
20), which was sometimes necessary to get this model to converge.
est <- netest(nw, formation, target.stats, coef.diss,
set.control.ergm = control.ergm(MCMLE.maxit = 100))Model diagnostics look similar to last time.
dx <- netdx(est, nsims = 10, ncores = 5, nsteps = 500,
nwstats.formula = ~edges + absdiff("age") + degree(0:6),
set.control.tergm =
control.simulate.formula.tergm(MCMC.burnin.min = 20000))
Network Diagnostics
-----------------------
- Simulating 10 networks
- Calculating formation statistics
- Calculating duration statistics
- Calculating dissolution statistics
print(dx)EpiModel Network Diagnostics
=======================
Diagnostic Method: Dynamic
Simulations: 10
Time Steps per Sim: 500
Formation Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SD
edges 1000 988.122 -1.188 25.453
absdiff.age 2000 1968.091 -1.595 80.112
degree0 80 87.802 9.753 9.704
degree1 NA 322.310 NA 15.629
degree2 NA 292.952 NA 14.737
degree3 NA 176.160 NA 12.416
degree4 NA 79.715 NA 9.582
degree5 NA 29.272 NA 5.752
degree6 NA 8.897 NA 3.028
Duration Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SD
edges 20 19.992 -0.042 0.158
Dissolution Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SD
edges 0.05 0.05 -0.228 0plot(dx)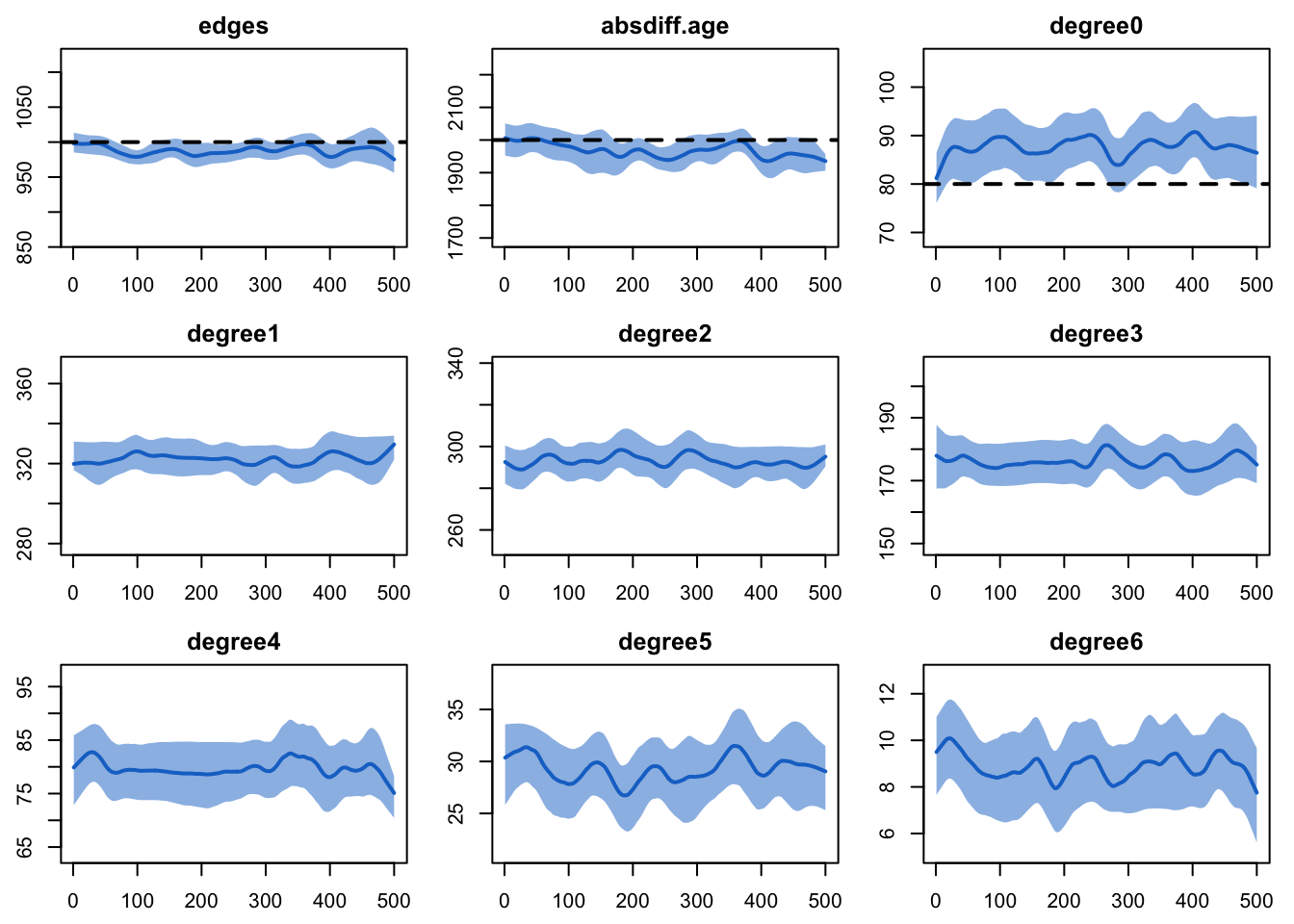
Epidemic Model Simulation
We are now using more realistic COVID parameters for disease
progression, based on the current literature and other models. Note that
the current parameters allow for 50% lower transmissibility in the
asymptomatic stage, age-varying clinical pathways, a PCR sensitivity of
80%, a diagnosis rate that is 20-fold higher for those with symptomatic
infection, and no rescreening. We have also prevented any case isolation
by setting the act.rate.dx.inter.time to
Inf.
param <- param.net(inf.prob = 0.1,
act.rate = 3,
departure.rates = dr_vec,
departure.disease.mult = 1000,
arrival.rate = 1/(365*85),
inf.prob.a.rr = 0.5,
act.rate.dx.inter.time = Inf,
act.rate.dx.inter.rr = 0.05,
# proportion in clinical pathway by age decade
prop.clinical = c(0.40, 0.25, 0.37, 0.42, 0.51, 0.59, 0.72, 0.76),
ea.rate = 1/4.0,
ar.rate = 1/5.0,
eip.rate = 1/4.0,
ipic.rate = 1/1.5,
icr.rate = 1/3.5,
pcr.sens = 0.8,
dx.rate.sympt = 0.2,
dx.rate.other = 0.01,
allow.rescreen = FALSE)
init <- init.net()For the control settings, it is necessary to define all the relevant
modules for our system, and input the associated functions. We will
simulate the model only over 100 days, with 10 simulations. Here we use
tergmLite, but this can be set to FALSE to retain the full
network data (these simulations will take a bit longer).
source("d5-s6-COVIDScreen-fx.R")
control <- control.net(type = NULL,
nsims = 10,
ncores = 5,
nsteps = 100,
infection.FUN = infect2,
progress.FUN = progress2,
dx.FUN = dx_covid,
aging.FUN = aging,
departures.FUN = dfunc2,
arrivals.FUN = afunc2,
resimulate.network = TRUE,
tergmLite = TRUE,
set.control.tergm =
control.simulate.formula.tergm(MCMC.burnin.min = 10000))The model is then simulated with netsim.
sim <- netsim(est, param, init, control)Model Analysis
Let’s print out the netsim object to review the available data variables.
simEpiModel Simulation
=======================
Model class: netsim
Simulation Summary
-----------------------
Model type:
No. simulations: 10
No. time steps: 100
No. NW groups: 1
Fixed Parameters
---------------------------
inf.prob = 0.1
act.rate = 3
departure.rates = 1.612192e-05 6.794521e-07 6.794521e-07 6.794521e-07
6.794521e-07 3.205479e-07 3.205479e-07 3.205479e-07 3.205479e-07 3.205479e-07
...
departure.disease.mult = 1000
arrival.rate = 3.223207e-05
inf.prob.a.rr = 0.5
act.rate.dx.inter.time = Inf
act.rate.dx.inter.rr = 0.05
prop.clinical = 0.4 0.25 0.37 0.42 0.51 0.59 0.72 0.76
ea.rate = 0.25
ar.rate = 0.2
eip.rate = 0.25
ipic.rate = 0.6666667
icr.rate = 0.2857143
pcr.sens = 0.8
dx.rate.sympt = 0.2
dx.rate.other = 0.01
allow.rescreen = FALSE
groups = 1
Model Functions
-----------------------
initialize.FUN
resim_nets.FUN
infection.FUN
departures.FUN
arrivals.FUN
nwupdate.FUN
prevalence.FUN
verbose.FUN
progress.FUN
dx.FUN
aging.FUN
Model Output
-----------------------
Variables: s.num i.num num ea.flow ar.flow eip.flow
ipic.flow icr.flow e.num a.num ip.num ic.num r.num nDx
nDx.pos nDx.pos.sympt nDx.pos.fn meanAge se.flow
total.deaths covid.deaths a.flow
Transmissions: sim1 ... sim10
Formation Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SD
edges 1000 900.374 -9.963 32.552
degree0 80 118.019 47.524 13.830
absdiff.age 2000 1952.704 -2.365 73.046
Dissolution Diagnostics
-----------------------
Not available when:
- `control$tergmLite == TRUE`
- `control$save.network == FALSE`
- dissolution formula is not `~ offset(edges)`Here is a plot of disease state sizes over time. The default plot makes it difficult to see the prevalence because the susceptible and recovered state sizes are much larger overall, so we plot just the three infectious states alone.
par(mfrow = c(1,2))
plot(sim)
plot(sim, y = c("a.num", "ip.num", "ic.num"), legend = TRUE)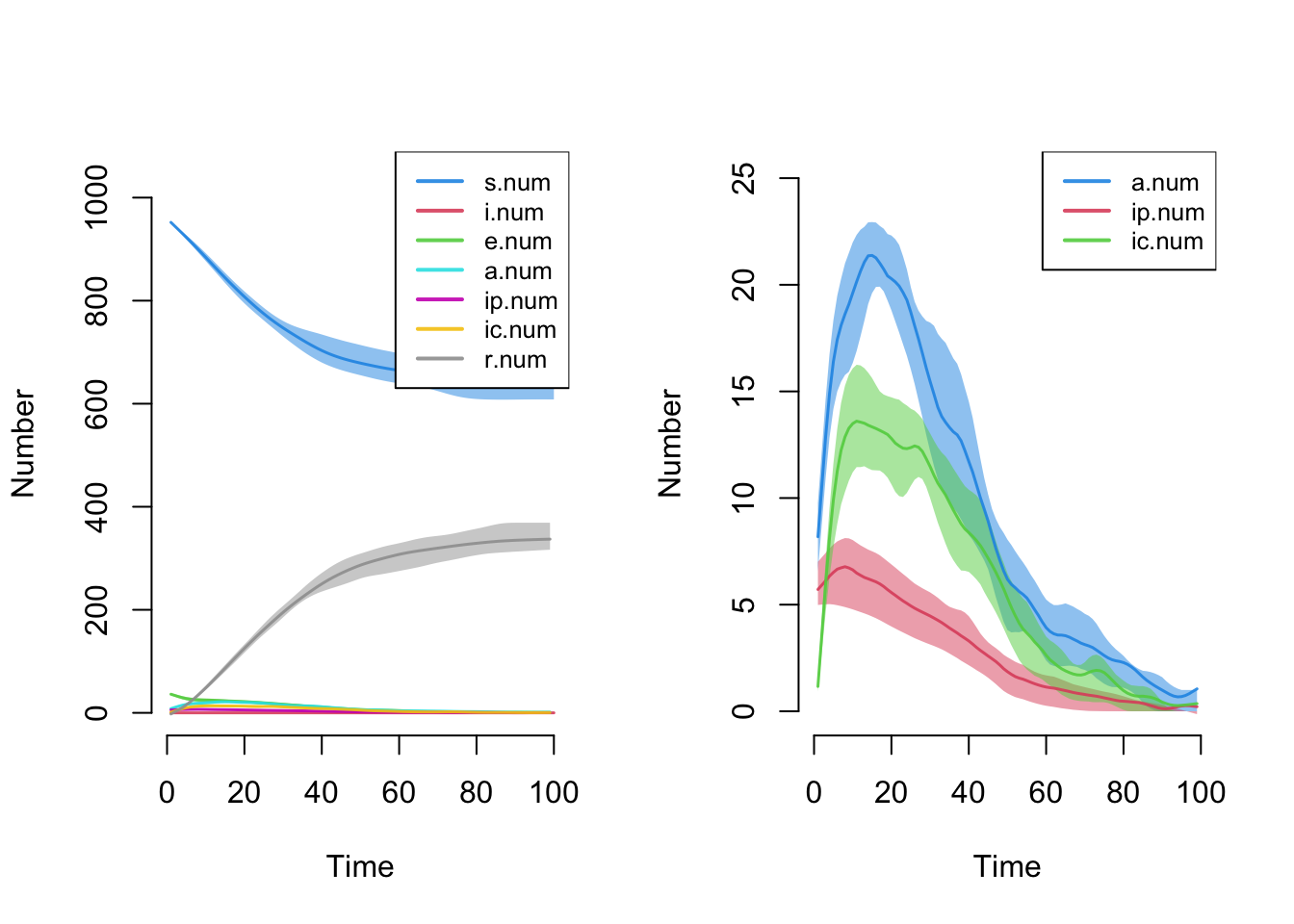
Here are the first three transitions after leaving the suceptible state.
par(mfrow = c(1, 1))
plot(sim, y = c("se.flow", "ea.flow", "eip.flow"), legend = TRUE)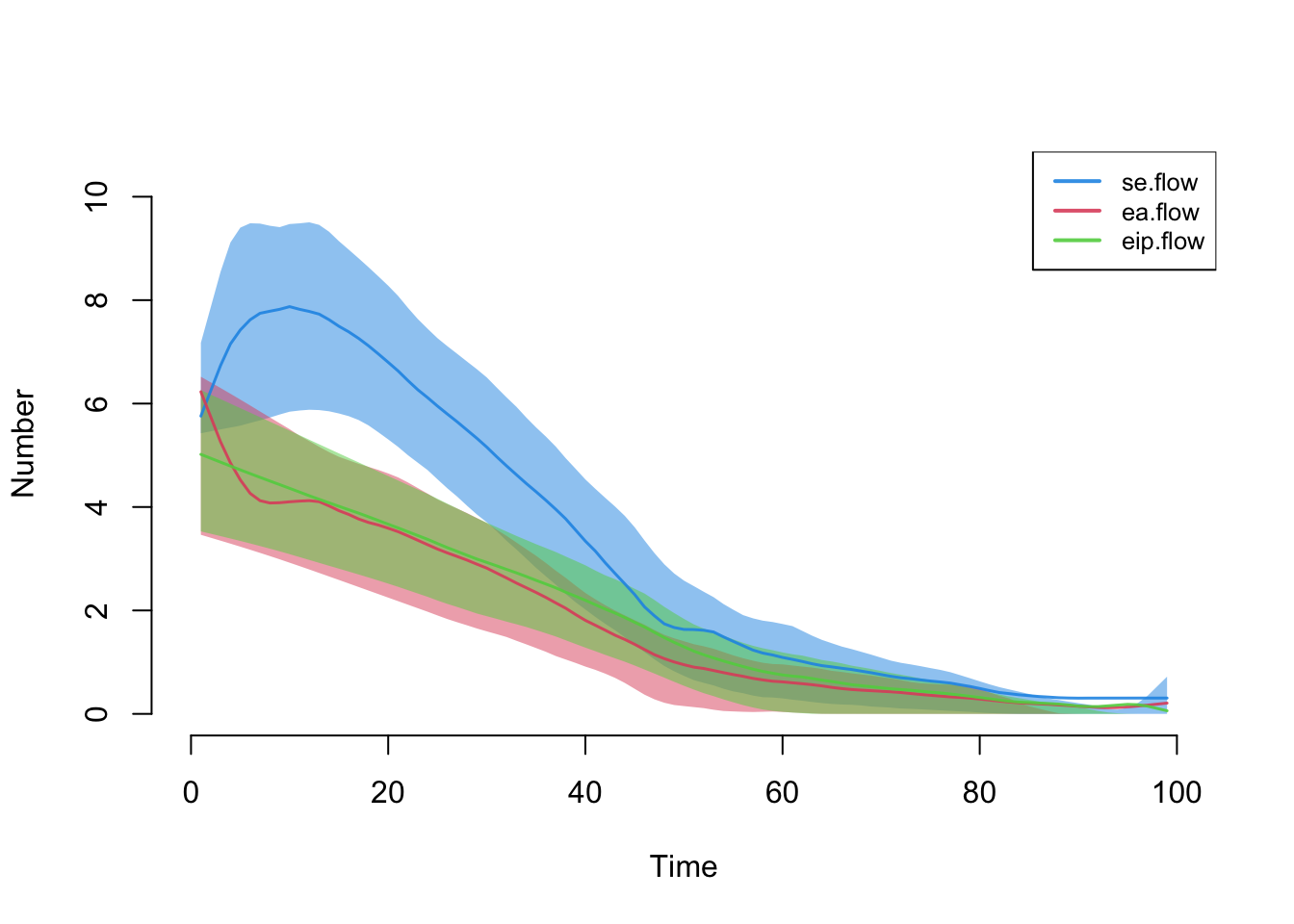
Finally, we can export the mean data, averaged across the 10 simulations.
df <- as.data.frame(sim, out = "mean")
head(df) time s.num i.num num ea.flow ar.flow eip.flow ipic.flow icr.flow e.num
1 1 950.0 0 1000.0 NaN NaN NaN NaN NaN NaN
2 2 944.7 0 1000.1 6.2 0.0 5.8 0.0 0.0 38.0
3 3 938.7 0 999.9 6.8 1.1 4.2 4.1 0.0 32.4
4 4 931.6 0 999.6 3.7 1.6 4.6 4.7 1.0 30.2
5 5 923.0 0 999.5 4.9 1.5 4.8 3.9 2.2 27.6
6 6 915.7 0 999.2 4.9 4.6 4.7 4.7 2.3 26.7
a.num ip.num ic.num r.num nDx nDx.pos nDx.pos.sympt nDx.pos.fn meanAge
1 NaN NaN NaN NaN NaN NaN NaN NaN NaN
2 6.2 5.8 0.0 0.0 9.9 0.4 0.0 0.0 42.31674
3 11.9 5.9 4.1 1.1 10.2 1.1 0.7 0.4 42.31525
4 14.0 5.8 7.5 3.7 10.4 1.5 1.4 0.5 42.30295
5 17.4 6.7 8.9 7.4 10.6 1.8 1.4 0.2 42.29917
6 17.7 6.7 11.1 14.3 10.7 2.0 1.3 0.7 42.28201
se.flow total.deaths covid.deaths a.flow
1 NaN NaN NaN NaN
2 5.4 0.0 0.0 0.1
3 6.1 0.3 0.3 0.1
4 7.1 0.3 0.3 0.0
5 8.7 0.3 0.2 0.2
6 7.3 0.3 0.3 0.0And calculate the average cumulative incidence.
sum(df$se.flow, na.rm = TRUE)[1] 307.7Last updated: 2022-07-07 with EpiModel v2.3.0