Tutorial: Feedback Through Nodal Attribute Changes
Day 4 | Network Modeling for Epidemics
This next tutorial will briefly demonstrate how changes to nodal attributes over time are another mechanism that results in feedback between the epidemic system and the dynamic network structure. In the context of diseases like HIV, partnership selection and activity level may vary based on disease status (more specifically, diagnosed disease status but we’ll ignore that complication in this model). Because disease status can change over time, any network model that references the disease status attribute must then be resimulated when the nodal attributes change. And these nodal attributes for disease status change as a function of the infections that results from the network structure. Therefore, we have feedback! This tutorial will walk through the parameterization and implications of this model.
Network Model
First, we will set up our network and then calculate our target statistics under the parameterization that people with infection have a lower mean degree than those without infection. This may be a function of behavioral change following disease diagnosis, which is commonly observed for HIV. We are not yet considering how they match up.
n <- 500
nw <- network_initialize(n)Parameterization
The initial prevalence in the network will be 20%. Note that we need
to specify a vertex attribute, which must be called status,
for this model. This is another “special” attribute on the network, like
group, that is treated differently from any other named
attribute. That is because status is the main attribute
within netsim that keeps track of the individual disease
status. We need to initialize the network like this with
status as an individual attribute specifically because it
will be a term within our TERGM; therefore, we will not randomly set the
infected number with init.net as we have in previous
tutorials.
Here, we assign exactly 100 nodes as infected, and randomly select which nodes those will be.
prev <- 0.2
infIds <- sample(1:n, n*prev)
nw <- set_vertex_attribute(nw, "status", "s")
nw <- set_vertex_attribute(nw, "status", "i", infIds)
get_vertex_attribute(nw, "status") [1] "s" "s" "s" "i" "i" "s" "s" "s" "s" "s" "i" "s" "s" "s" "s" "s" "s" "i"
[19] "s" "s" "i" "s" "s" "s" "s" "s" "s" "i" "s" "s" "s" "s" "s" "i" "s" "s"
[37] "s" "s" "s" "s" "s" "s" "s" "s" "s" "i" "s" "i" "s" "s" "s" "s" "s" "s"
[55] "s" "i" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "i" "s" "i" "s" "s" "s"
[73] "s" "s" "s" "s" "s" "i" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "i" "s"
[91] "i" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "i" "s" "i"
[109] "s" "s" "s" "s" "i" "i" "s" "s" "s" "i" "s" "s" "s" "s" "s" "s" "i" "s"
[127] "s" "s" "s" "s" "s" "s" "s" "s" "i" "s" "s" "s" "s" "i" "s" "s" "s" "i"
[145] "s" "s" "i" "s" "s" "s" "s" "s" "s" "i" "s" "s" "s" "i" "s" "i" "i" "s"
[163] "s" "s" "i" "s" "s" "s" "i" "s" "s" "s" "i" "i" "i" "s" "s" "s" "s" "i"
[181] "i" "s" "s" "s" "i" "s" "i" "s" "s" "s" "s" "s" "s" "s" "s" "i" "s" "i"
[199] "i" "i" "s" "i" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "i" "s"
[217] "s" "s" "i" "s" "s" "i" "s" "s" "s" "s" "s" "s" "i" "s" "s" "i" "s" "s"
[235] "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "i" "s" "s" "s" "s" "s" "s"
[253] "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "i" "i" "s" "i" "s" "s" "s"
[271] "i" "s" "s" "s" "s" "s" "s" "i" "s" "i" "i" "s" "s" "i" "s" "i" "s" "s"
[289] "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "i" "s" "i" "s" "s" "s" "s" "i"
[307] "s" "i" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "i" "s" "i" "s"
[325] "s" "s" "i" "s" "i" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "i" "s" "s"
[343] "s" "s" "i" "i" "s" "s" "s" "i" "s" "s" "s" "i" "s" "s" "s" "s" "s" "s"
[361] "s" "s" "s" "s" "s" "s" "s" "s" "i" "s" "s" "s" "i" "s" "s" "s" "s" "s"
[379] "s" "s" "s" "s" "i" "i" "s" "s" "s" "s" "s" "i" "i" "s" "i" "s" "s" "s"
[397] "s" "s" "i" "s" "s" "s" "s" "s" "s" "i" "s" "s" "s" "s" "s" "s" "s" "i"
[415] "s" "s" "i" "s" "s" "s" "i" "s" "s" "s" "i" "s" "s" "s" "s" "s" "s" "s"
[433] "s" "s" "s" "s" "s" "s" "s" "i" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s"
[451] "i" "i" "s" "i" "s" "s" "s" "s" "s" "i" "s" "s" "s" "s" "i" "s" "s" "s"
[469] "s" "i" "s" "i" "s" "i" "s" "i" "s" "i" "s" "s" "s" "s" "s" "i" "s" "s"
[487] "s" "s" "s" "s" "s" "s" "s" "i" "i" "i" "s" "s" "i" "s"A nodefactor term will allow the mean degree of the
infected persons to differ from that of susceptible persons. In the
previous tutorial, we calculated the nodefactor target
statistic as the mean degree of a group times the size of the group.
Another way of expressing that is a count of the number of times a
member of a group, here an infected person or susceptible person, show
up in an edge. And this is just the the group mean degree times the
group size; here, the group size is defined by the disease prevalence,
prev, variable specified above.
mean.deg.inf <- 0.3
inedges.inf <- mean.deg.inf * n * prev
inedges.inf[1] 30mean.deg.sus <- 0.8
inedges.sus <- mean.deg.sus * n * (1 - prev)
inedges.sus[1] 320The number of edges then is the sum of these two
nodefactor statistics divided by 2 (because
nodefactor is an expression of nodes).
edges <- (inedges.inf + inedges.sus)/2
edges[1] 175Next, let’s move on to parameterizing mixing by disease status. In
this theoretically parameterized model, here again it is helpful to
think about this in terms of what the expected statistic would be in the
absence of any preferential or assortative mixing. That is, what is the
value of the nodematch target statistic under a
proportional (random) mixing model? We worked this out in the previous
tutorial for the case where there were equally sized groups with the
same mean degree. It gets more complicated here because the groups are
of different sizes, and different activity levels. There are different
ways to find this solution.
The exact solution: from population genetics, the Hardy-Weinberg Principle. This code below fills out a two-by-two table that contains the probabilities of a S-S, I-I, and S-I pair. The proportion of partnerships that are matched on status is the diagonal of the table, which is the sum of the S-S and I-I probabilities.
p <- inedges.sus/(edges*2)
q <- 1 - p
nn <- p^2
np <- 2*p*q
pp <- q^2
round(nn + pp, 3)[1] 0.843A simulation-based solution: we estimate an ERGM in which
there is no nodematch term but heterogeneity in activity,
then simulate from that fitted model to calculate the expected number of
matched edges. The proportion of matched edges is that number over the
total edges.
fit <- netest(nw,
formation = ~edges + nodefactor("status"),
target.stats = c(edges, inedges.sus),
coef.diss = dissolution_coefs(~offset(edges), duration = 1))
sim <- netdx(fit, dynamic = FALSE, nsims = 1e4,
nwstats.formula = ~edges + nodematch("status"))
Network Diagnostics
-----------------------
- Simulating 10000 networks
- Calculating formation statisticsstats <- get_nwstats(sim)
head(stats) sim edges nodefactor.status.s nodematch.status
1 1 153 280 127
2 2 167 302 139
3 3 160 296 142
4 4 162 299 139
5 5 175 331 156
6 6 159 290 131round(mean(stats$nodematch.status/stats$edges), 3)[1] 0.843The main substantive finding here is that 84% of relations are expected to be within the same disease status group under a proportional mixing group, even without a behavioral preference for assortative mixing. This is because suceptible persons are a larger group in the population, and have more relationships per-capita.
Let us now imagine that there are in fact slightly more within-group ties than expected by chance:
nmatch <- edges * 0.91Estimation
This tutorial will compare two models to assess the impact of behavior driven by disease status on epidemic trajectories:
- Model 1 features two forms of seroadaptive behavior: different levels of activity by disease status, and matching on status.
- Model 2 has neither, so is just a Bernoulli model with same mean degree as Model 1.
Model 1
The network model with serosorting will include terms for both the
number of times susceptible persons show up in an edge, as well as the
number of node-matched edges overall. It is unnecessary to specify the
nodefactor term for the susceptible persons because that is
a function of total edges and the nodefactor term for the
infected persons (the base level is always the first in alphabetical or
numerical order, so “i” for our status variable level in this case). The
average partnership duration in both models will be 50 time steps.
formation <- ~edges + nodefactor("status") + nodematch("status")
target.stats <- c(edges, inedges.sus, nmatch)
coef.diss <- dissolution_coefs(dissolution = ~offset(edges), 50)
est <- netest(nw, formation, target.stats, coef.diss)We run the network diagnostics on the model.
dx <- netdx(est, nsims = 10, nsteps = 500, ncores = 5,
nwstats.formula = ~edges +
meandeg +
nodefactor("status", levels = NULL) +
nodematch("status"), verbose = FALSE)
dxEpiModel Network Diagnostics
=======================
Diagnostic Method: Dynamic
Simulations: 10
Time Steps per Sim: 500
Formation Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SD
edges 175.00 173.977 -0.584 15.474
meandeg NA 0.696 NA 0.062
nodefactor.status.i NA 29.417 NA 5.621
nodefactor.status.s 320.00 318.538 -0.457 29.481
nodematch.status 159.25 158.020 -0.772 14.978
Duration Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SD
edges 50 49.872 -0.256 1.193
Dissolution Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SD
edges 0.02 0.02 -0.006 0.001plot(dx)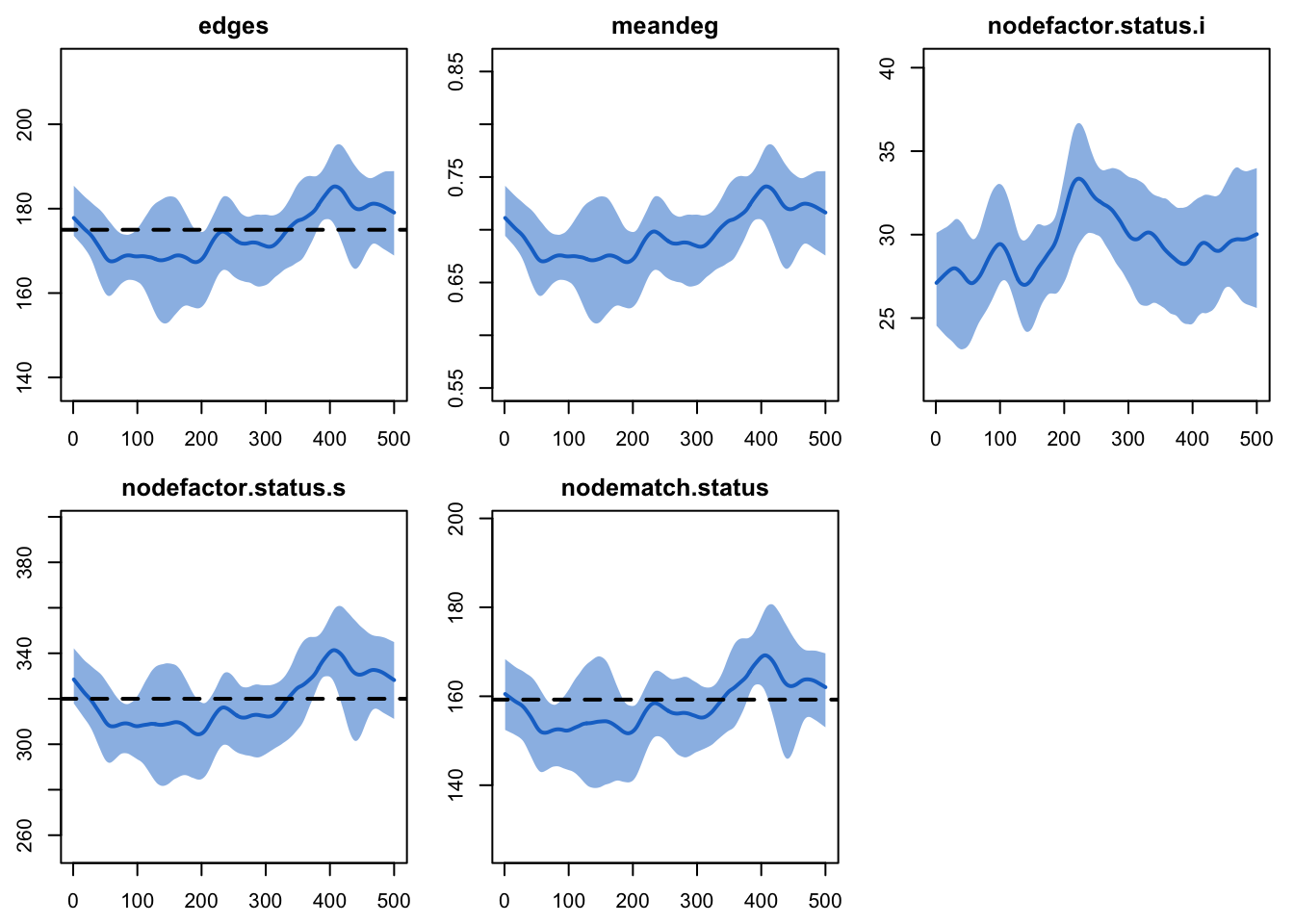
plot(dx, type = "dissolution")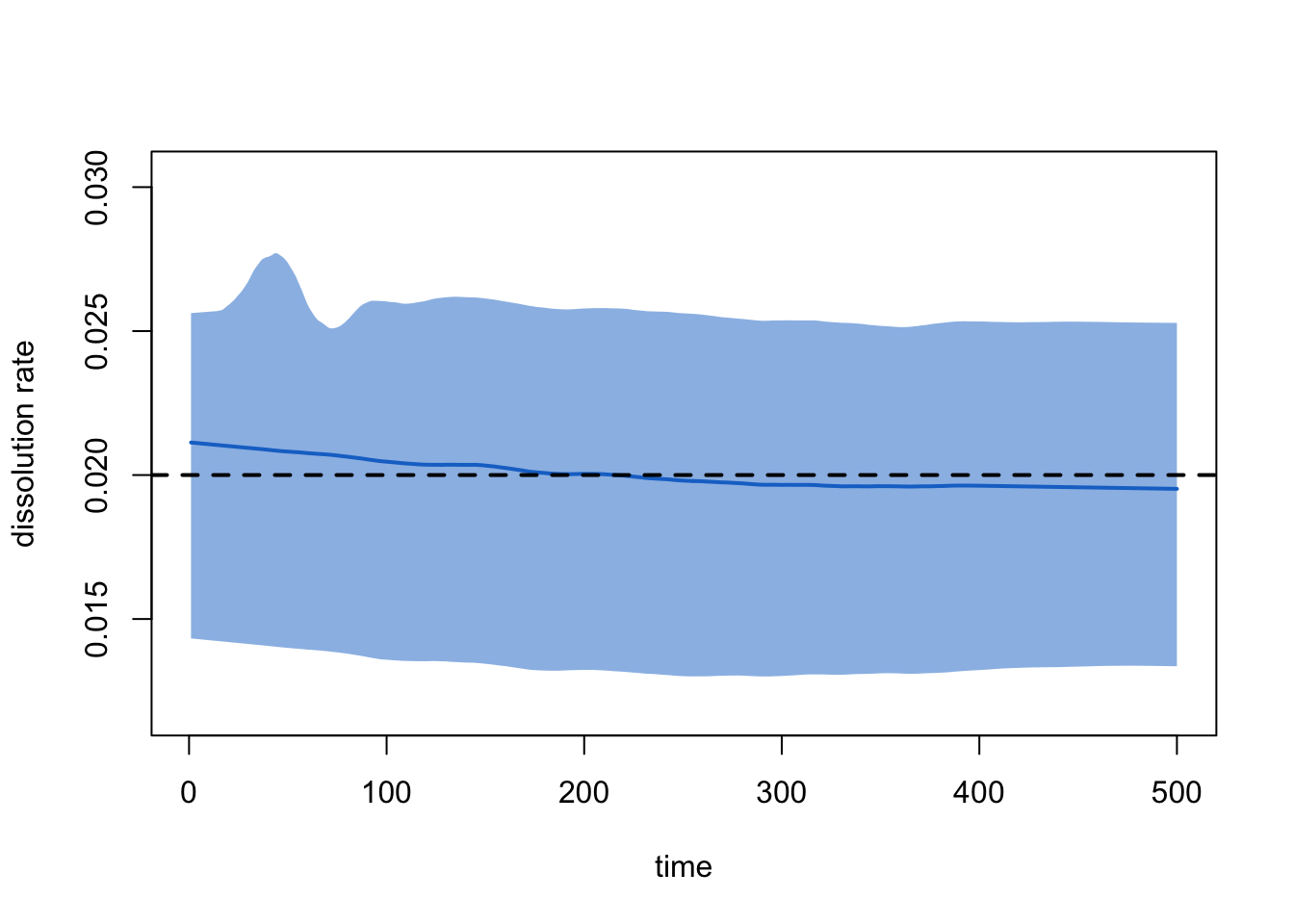
Model 2
The second model will include only an edges term, so no serosorting
behavior but same amount of activity among nodes. We are recycling the
nw object with the status attribute set from
above.
est2 <- netest(nw, formation = ~edges, target.stats = edges, coef.diss)After estimation, the diagnostics here look fine too. Compare the
nodefactor and nodematch simulations here to
those in the Model 1 diagnostics: more edges for infected persons, and
more discordant (S-I) edges.
dx2 <- netdx(est2, nsims = 10, nsteps = 1000, ncores = 5,
nwstats.formula = ~edges +
meandeg +
nodefactor("status", levels = NULL) +
nodematch("status"), verbose = FALSE)
dx2EpiModel Network Diagnostics
=======================
Diagnostic Method: Dynamic
Simulations: 10
Time Steps per Sim: 1000
Formation Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SD
edges 175 174.732 -0.153 13.439
meandeg NA 0.699 NA 0.054
nodefactor.status.i NA 69.524 NA 9.476
nodefactor.status.s NA 279.940 NA 22.972
nodematch.status NA 118.668 NA 10.931
Duration Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SD
edges 50 49.799 -0.402 0.855
Dissolution Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SD
edges 0.02 0.02 0.378 0plot(dx2)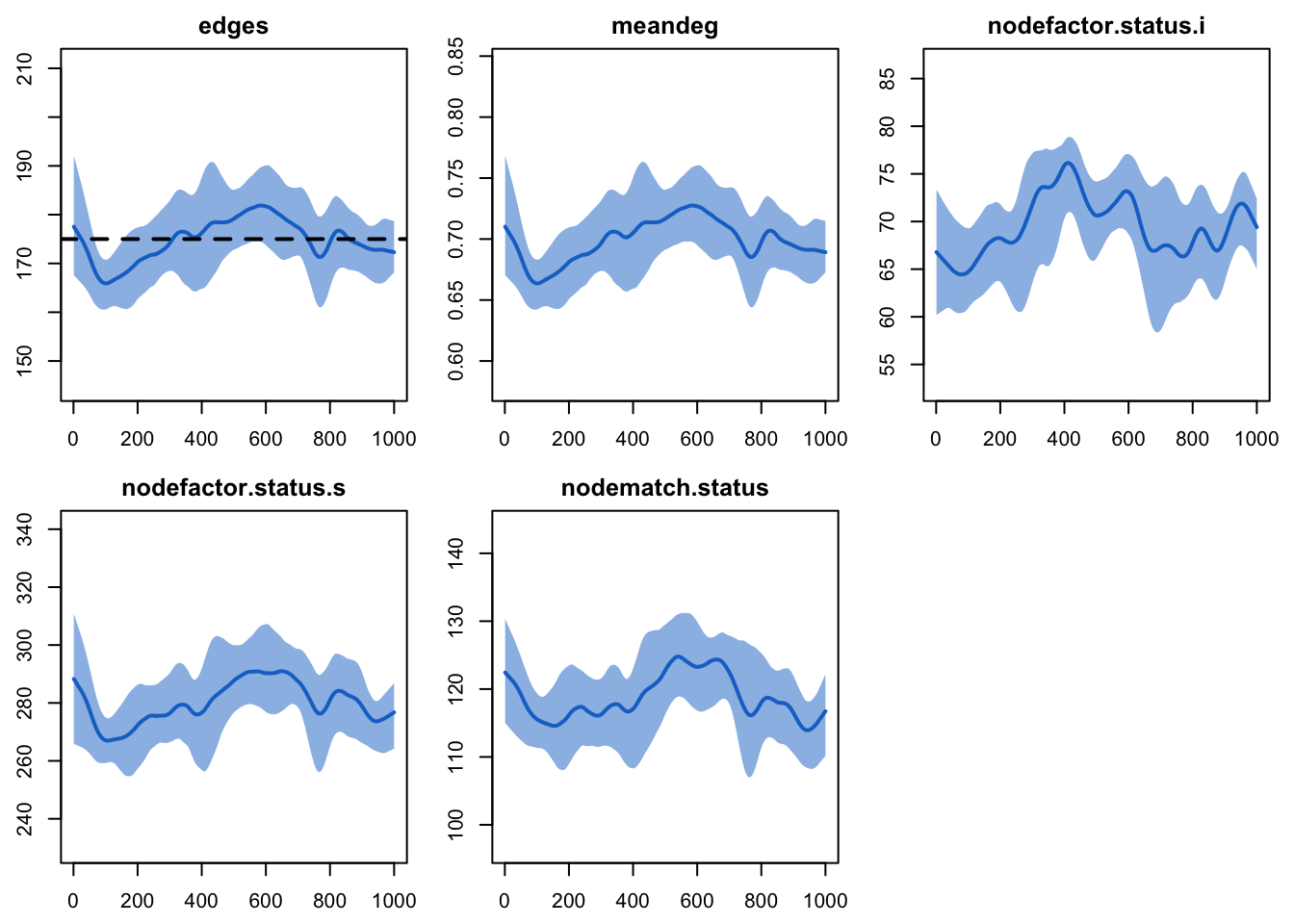
Epidemic Model
For the epidemic model, we will simulate an SI disease, with our two counterfactual network models. The first model will use the serosorting network model, and the second will be the random Bernoulli model.
Model 1
The model will only include one named parameter, for the transmission probability per contact.
param <- param.net(inf.prob = 0.03)The initial conditions are now passed through to the epidemic model
not through init.net as with previous examples, but through
the netest object that contains the original starting
network with the vertex attributes for status. However, because
netsim will still be expecting an initial conditions list,
we need to create an empty object as a placeholder.
init <- init.net()For the control settings, we monitor the same network statistics as
we did in the network diagnostics above. The
resimulate.networks argument must be set to
TRUE because the network needs to be updated at each time
step. In this model, we will use the tergmLite approach since we do not
need to monitor individual-level network histories.
control <- control.net(type = "SI", nsteps = 500, nsims = 5, ncores = 5,
resimulate.network = TRUE, tergmLite = TRUE,
nwstats.formula = ~edges +
meandeg +
nodefactor("status", levels = NULL) +
nodematch("status"))Here, we run the model. We will return to it to compare output later.
sim <- netsim(est, param, init, control)Model 2
The second model includes the same epidemic parameters as Model 1, so all that we need to change is the first parameter for the different network object.
sim2 <- netsim(est2, param, init, control)Results
Here we’ll look at the epidemic results first and then the network diagnostics, because the network statistics will be a function of the epidemiology.
Here we see that the serosorting model grows much less quickly than the random model. The reasons are that nodes lower their mean degree upon infection, and therefore have fewer partners over time. They also tend to preferentially partner with other infecteds.
par(mfrow = c(1,2))
plot(sim, main = "Seroadaptive Behavior")
plot(sim2, main = "No Seroadaptive Behavior")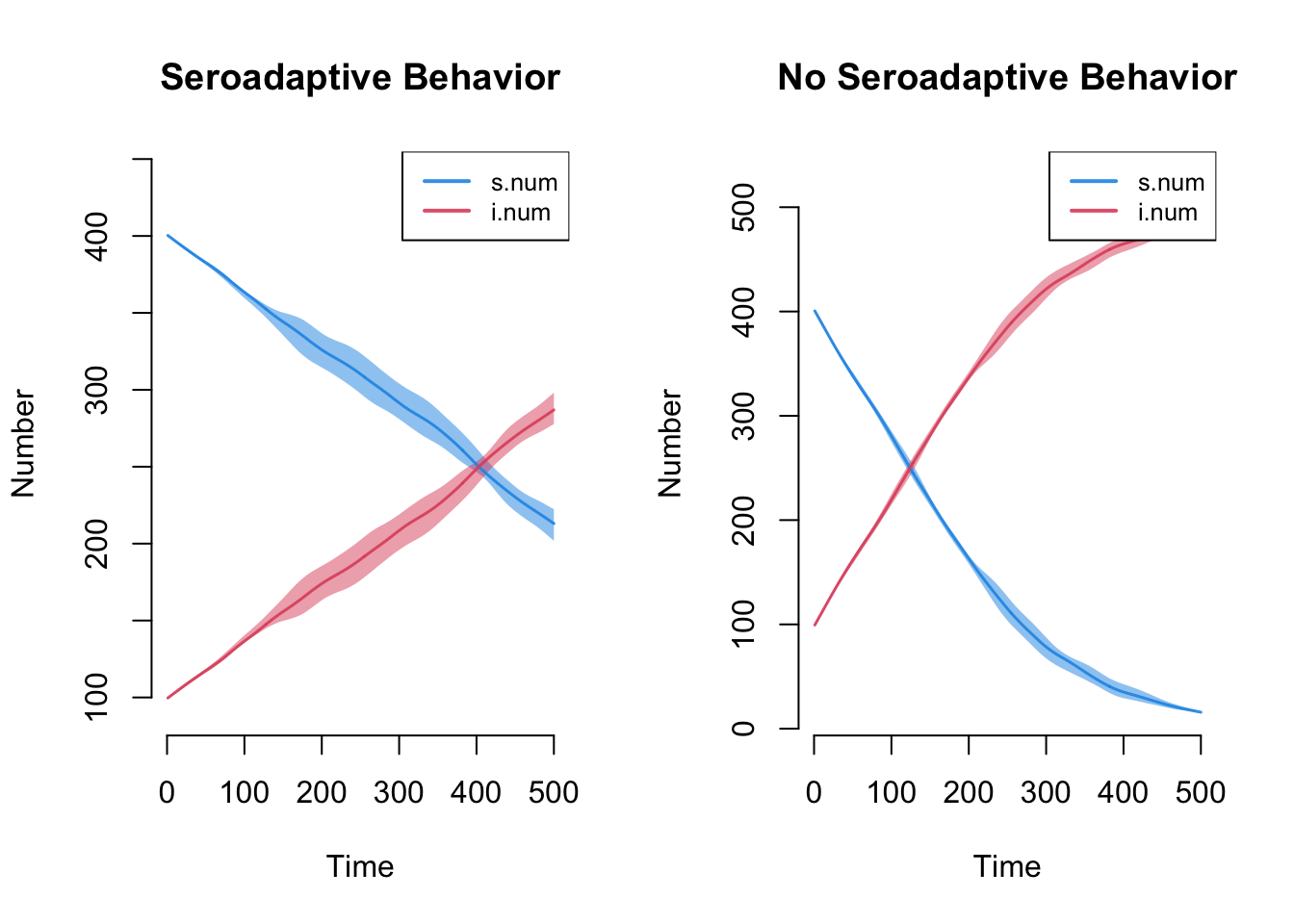
Another method to show the relative difference is to plot the two epidemic trajectories together. This requires a custom legend.
par(mfrow = c(1,1))
plot(sim, y = "i.num", popfrac = TRUE, sim.lines = FALSE, qnts = 1)
plot(sim2, y = "i.num", popfrac = TRUE, sim.lines = FALSE, qnts = 1,
mean.col = 2, qnts.col = 2, add = TRUE)
legend("topleft", c("Serosort", "Non-Serosort"), lty = 1, lwd = 3,
col = c(4, 2), cex = 0.9, bty = "n")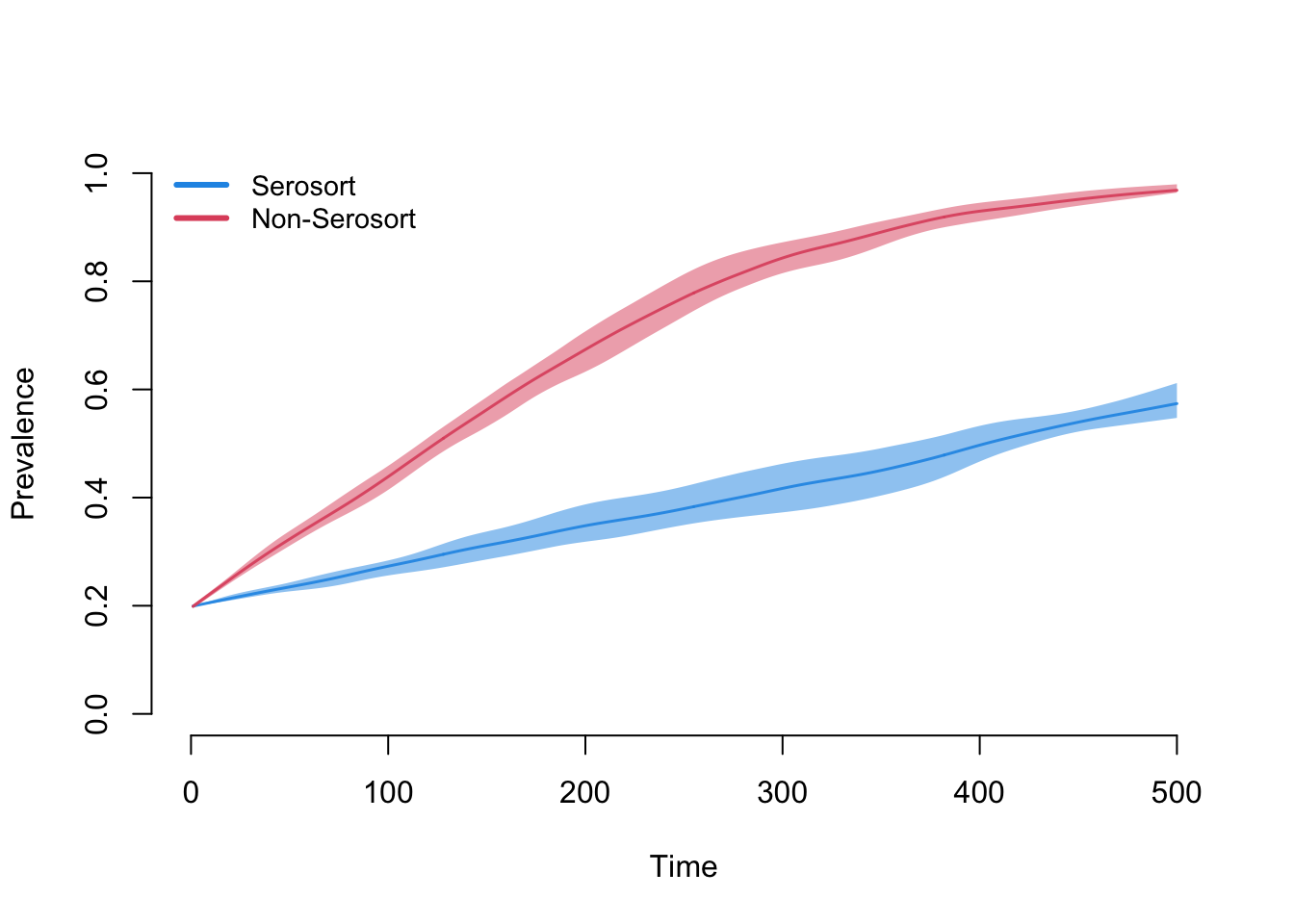
Now, here are the network statistics that we monitored in Model 1. In contrast to our previous tutorials, where we expected stochastic variation around the targets to be preserved over time, here every network statistic varies.
plot(sim, type = "formation")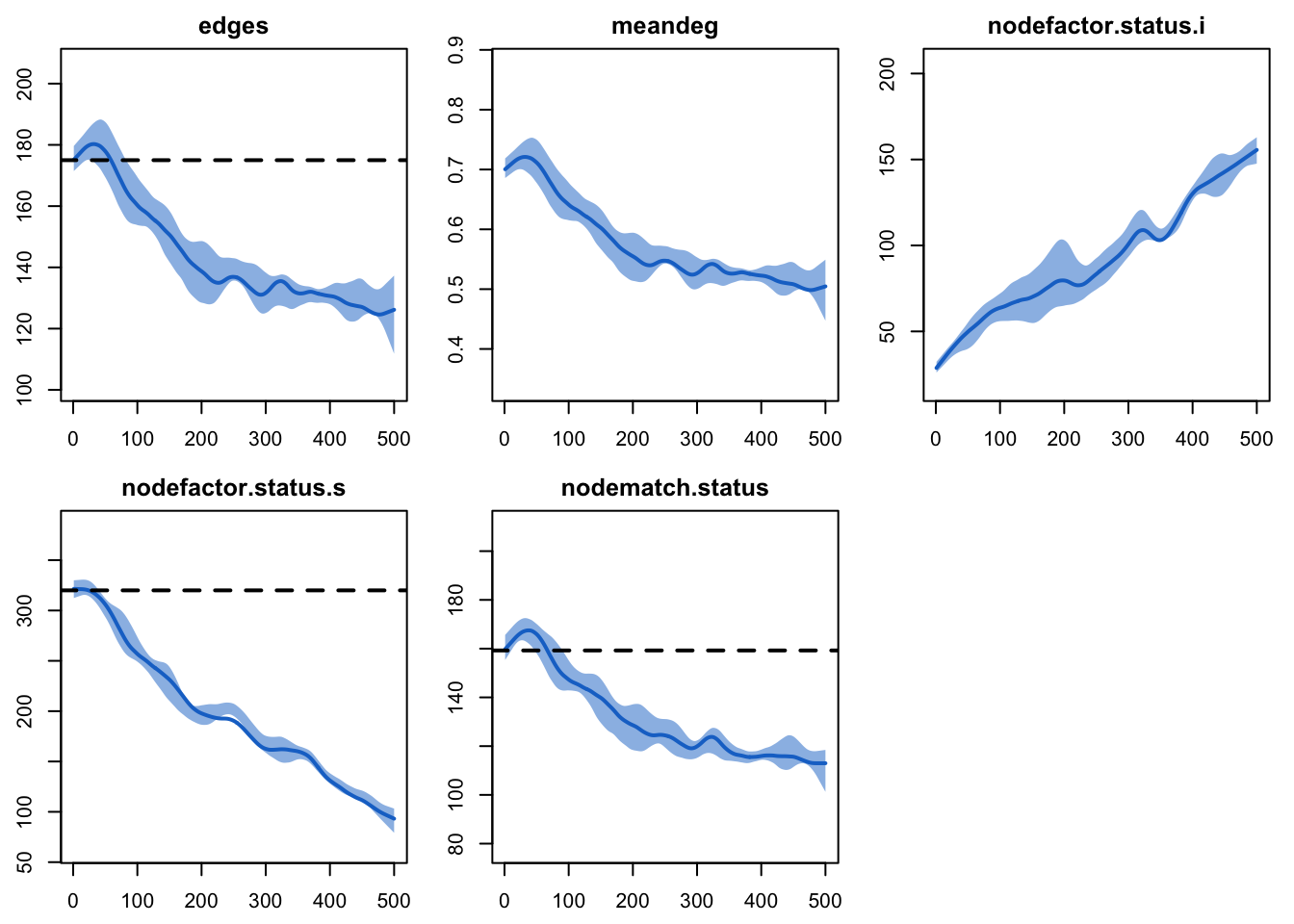
Notice first that the nodefactor statistics are moving
in opposite directions: as the prevalence of disease increases from 20%
to approximately 50% at time 500, the number of infected nodes in an
edge increases. The quantity preserved is not the number of
infected nodes in an edge that we set as a target (30 nodes); rather, it
is the log-odds of an infected node in an edge conditional on other
terms in the model.
plot(sim, type = "formation",
stats = c("nodefactor.status.s",
"nodefactor.status.i"))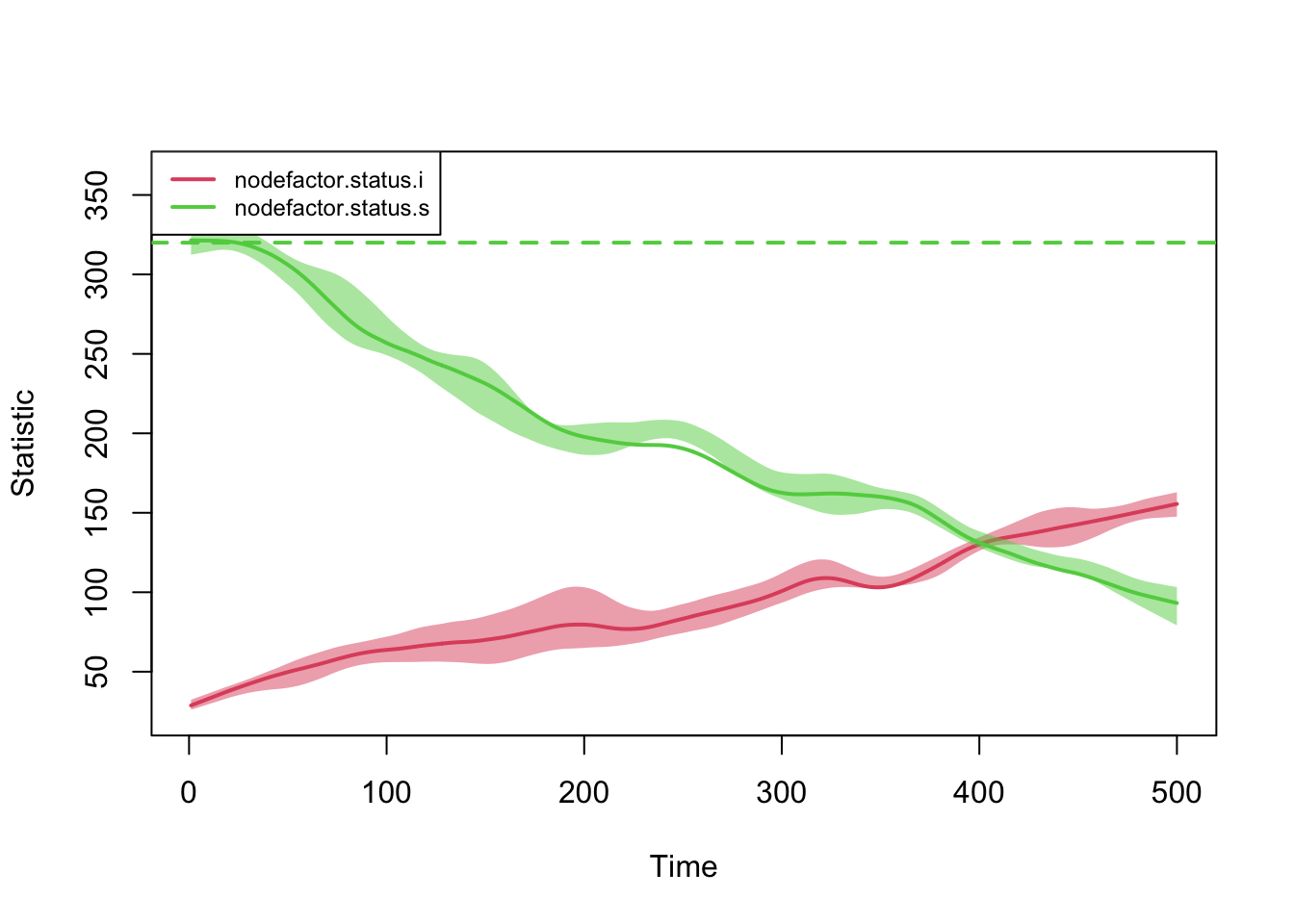
Second, note that the total edges and node-matched edges decline over
time. This plot shows those two statistics from one simulation only for
clarity. Ordinarily the mean degree is preserved even in a population
with drastically changing size, due to the network density correction
that automatically occurs in netsim.
plot(sim, type = "formation",
stats = c("edges", "nodematch.status"),
sims = 1, sim.lwd = 2)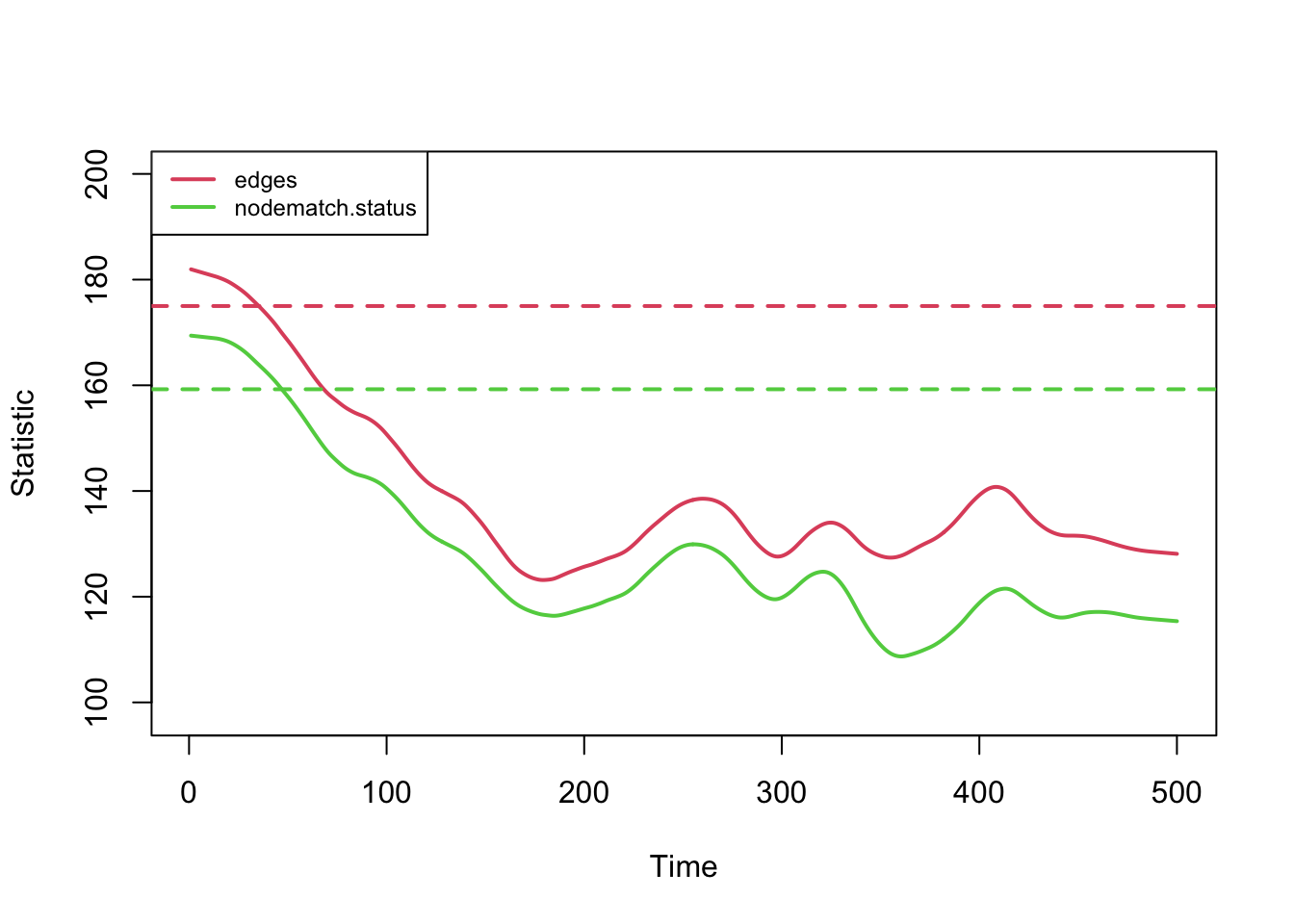
But in this case, the edges and mean degree are shrinking because the number of nodes in the network with the same status is steadily increasing, which draws the node match statistic lower since there are fewer susceptible-susceptible pairs available. Since the edges is a constant multiple of node-matched edges, they move together.
After looking at so many models where the target statistics were preserved throughout the simulation, this may seem like odd or undesirable behavior here. If it does, think about the main assumption we began with: men who are infected tend to have lower rates of partnering than men who are not infected. Perhaps this is because they are ill, or because they are trying to protect others. If this is the case, then what should we expect to happen to the overall rate of partnering as the proportion of men who are infected increases? Presumably it should go down, which is precisely what we see.
This behavior does mean that it can be difficut to tease apart the different contributions of serosorting to the disease dynamics that we see. How much of serosorting’s effect on lowering transmission came from the rate of overall partner reductions for infected men, and how much came from the homophily effect where infected men partner with each other relatively more? Although we included both in our model (through the nodefactor and nodematch terms, respectively), one could easily consider intermediate models that only included one term or the other, and then compare the results of each to the two models we already considered. We would then have a sense of the individual effects of each of these behavioral components, as well as their combined effect. Is the latter additive, less than additive, or more than additive (i.e. synergistic?)
Last updated: 2022-07-07 with EpiModel v2.3.0